Question

Find the magnitude and direction of the resultant of two vectors \[A\] and \[B\] in terms of their magnitudes and angle \[\theta \] between them.

Answer 1

Hint: In order to solve this question, we are first going to consider the two vectors, and consider the magnitudes for them. Now, we will consider the parallelogram with the two vectors \[A\] and \[B\], and the resultant is given by the diagonal of the parallelogram. Then, the magnitude and direction of the resultant are found.

Formula used:
The Pythagoras theorem is given by,
\[O{C^2} = C{D^2} + D{O^2}\]
Where, \[OC\] is the hypotenuse, \[CD\] and \[DO\] are base and perpendicular.

Complete answer:
It is given that there are two vectors \[A\] and \[B\], such that their magnitudes are
$ \left| A \right| = a \\
  \left| B \right| = b \\ $

The angle between them is \[\theta \]
So, if the resultant of these two vectors is taken as \[C\]
Then,
\[A + B = C\]
Now, to find the magnitude and the direction, consider the parallelogram \[OABC\] with \[D\] as the foot of the perpendicular as shown in the figure

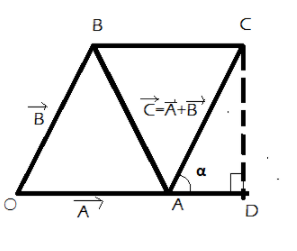
Now, in triangle \[OCD\], if we apply the Pythagoras theorem,
\[O{C^2} = C{D^2} + D{O^2}\]
Solving this further, we get
\[OC = \sqrt {O{A^2} + A{D^2} + 2 \cdot OA \cdot AD + C{D^2}} \]
Putting the values,
\[OC = \sqrt {{a^2} + {b^2} + 2 \cdot a \cdot b\cos \alpha } \]
Where,\[AD = AC\cos \alpha = b\cos \alpha \]
Thus, the magnitude of the resultant vector is
\[c = \sqrt {{a^2} + {b^2} + 2ab\cos \alpha } \]
Now, finding the direction, we get
Given that \[C\] makes an angle \[\theta \] with \[A\],
\[\theta = {\tan ^{ - 1}}\left( {\dfrac{{b\sin \alpha }}{{a + b\cos \alpha }}} \right)\]
Hence, the magnitude and direction of the resultant are given by
 $ c = \sqrt {{a^2} + {b^2} + 2ab\cos \alpha } \\
  \theta = {\tan ^{ - 1}}\left( {\dfrac{{b\sin \alpha }}{{a + b\cos \alpha }}} \right) \\ $

Note: It is important to note that the triangular law of addition has been applied in this question, for the vectors \[A\] and \[B\],
\[A + B = C\]
According to the triangle law of vector addition:
Triangle law of vector addition states that when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector.