Question

Find the inclination of a line whose slope is
A. \[-1\]
B. \[-\sqrt{3}\]

Answer 1

Hint: To solve this question, we will find the value of angle of tangent by putting \[m=\tan \theta \] equals to -1 and \[-\sqrt{3}\]. We know that tan ( - x) = - tanx. So, after finding the angle of inclination, we will draw the graphs by plotting straight line passing through origin and making angles with x – axis in anti – clockwise.

Complete step by step answer:
Let us understand the concepts. Use the fact that the slope of the line can also be represented as the tangent of the angle which the line makes with the positive x-axis when going anticlockwise from the x-axis. The value of m gives the slope of the line and then equate it to the tangent of the angle which the line makes with the positive x-axis when going anticlockwise from the x-axis as follows
\[m=\tan \theta \]
Here \[\theta \] is the angle that the line makes with the positive x-axis when going anticlockwise from the x-axis and m is the slope of the line which is inclined to the x-axis with the mentioned angle.
As mentioned in the question, we have to find the slope of the line which makes the given angle with the x-axis when going anticlockwise from the x-axis.
A. \[-1\]
We know that the slope of the line can be calculated as follows
\[\begin{align}
  & \Rightarrow m=\tan \theta \\
 & \Rightarrow -1=\tan \left( \theta \right) \\
 & \Rightarrow \theta ={{\tan }^{-1}}\left( -1 \right) \\
 & \Rightarrow \theta =-\dfrac{\pi }{4}=-{{45}^{\circ }}={{135}^{\circ }} \\
\end{align}\]

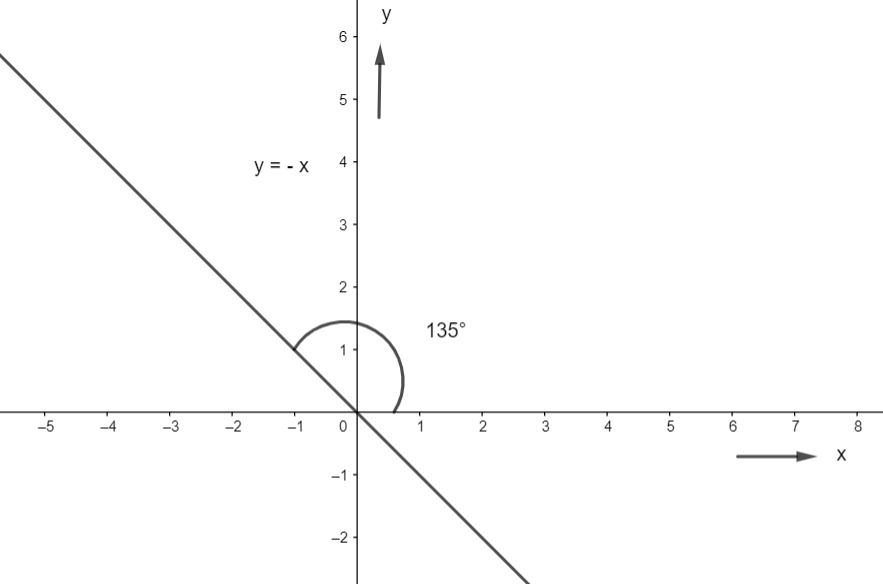
Hence, the angle of inclination of the line which has the mentioned slope, with the x-axis, is \[{{135}^{\circ }}\] .

B. \[-\sqrt{3}\]
We know that the slope of the line can be calculated as follows
\[\begin{align}
  & \Rightarrow m=\tan \theta \\
 & \Rightarrow -\sqrt{3}=\tan \theta \\
 & \Rightarrow \theta ={{\tan }^{-1}}-\sqrt{3} \\
 & \Rightarrow \theta =-{{\tan }^{-1}}\sqrt{3} \\
 & \Rightarrow \theta =-\dfrac{\pi }{3}={{120}^{\circ }} \\
\end{align}\]

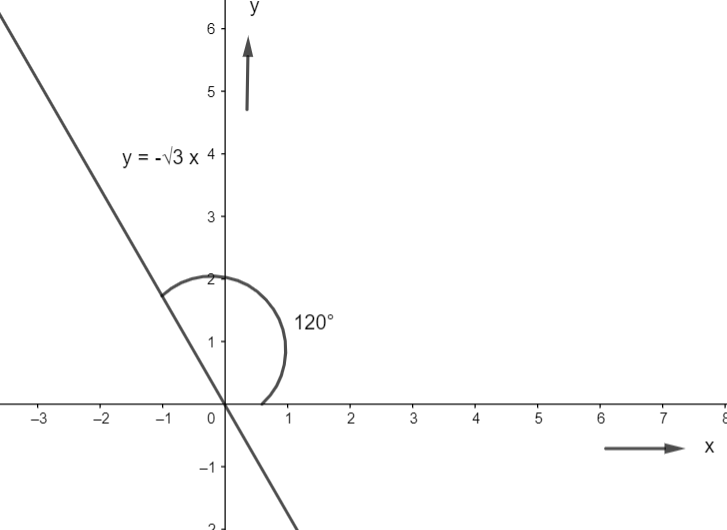
Hence, the angle of inclination of the line which has the mentioned slope, with the x-axis, is \[{{120}^{\circ }}\].

Note: The students can make an error if they don’t know about the formulae that are given in the hint as without knowing them one can never get to the correct answer. Here, keeping a check on the direction of the angle (either clockwise or anti-clockwise) is very important as it can give a wrong answer if not kept in mind. Also, it is important to know the basic values and the basic properties of tangent function and inverse tangent function for solving this question as without knowing them one can never get to the correct answer.