Question

Find the general solution of the equation $\cos \theta =-\dfrac{1}{2}$ is
A. $\theta =n\pi \pm \dfrac{2\pi }{3},n\in \mathbb{Z}$
B. $\theta =2n\pi \pm \dfrac{2\pi }{3},n\in \mathbb{Z}$
C. $\theta =n\pi \pm \dfrac{\pi }{3},n\in \mathbb{Z}$
D. none of these

Answer 1

Hint: We first find the principal value of x for which $\cos \theta =-\dfrac{1}{2}$. In that domain, equal value of the same ratio gives equal angles. We find the angle value for $\theta $. At the end we also find the general solution for the equation $\cos \theta =-\dfrac{1}{2}$.

Complete step by step solution:
It’s given that $\cos \theta =-\dfrac{1}{2}$. The value in fraction is $-\dfrac{1}{2}$. We need to find $\theta $ for which $\cos \theta =-\dfrac{1}{2}$.
We know that in the principal domain or the periodic value of $0\le x\le \pi $ for $\cos x$, if we get $\cos a=\cos b$ where $0\le a,b\le \pi $ then $a=b$.
We have the value of $\cos \left( \dfrac{2\pi }{3} \right)$ as $-\dfrac{1}{2}$. $0<\dfrac{2\pi }{3}<\pi $.
Therefore, \[\cos \theta =-\dfrac{1}{2}=\cos \left( \dfrac{2\pi }{3} \right)\] which gives \[\theta =\dfrac{2\pi }{3}\].
We need to find the general solution then the domain changes to $-\infty \le x\le \infty $. In that case we have to use the formula $x=2n\pi \pm a$ for $\cos \left( x \right)=\cos a$ where $0\le x\le \pi $. For our given problem $\cos \theta =-\dfrac{1}{2}$, the general solution will be $\theta =2n\pi \pm \dfrac{2\pi }{3}$. Here $n\in \mathbb{Z}$.

Note:
We also can show the solutions (primary and general) of the equation $\cos \theta =-\dfrac{1}{2}$ through a graph. We take $y=\cos \theta =-\dfrac{1}{2}$. We got two equations: $y=\cos \theta $ and $y=-\left( \dfrac{1}{2} \right)$. We place them on the graph and find the solutions as their intersecting points.

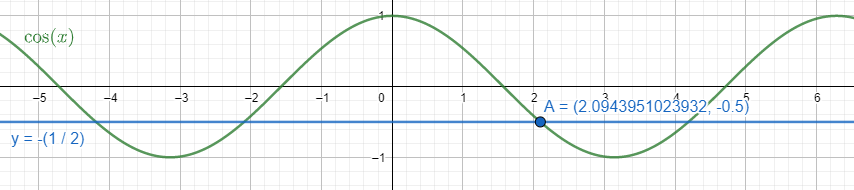
We can see the primary solution in the interval $0\le \theta \le \pi $ is the point A as $\theta =\dfrac{2\pi }{3}$.
All the other intersecting points of the curve and the line are general solutions.