Question

Find the equivalent resistance between A and B

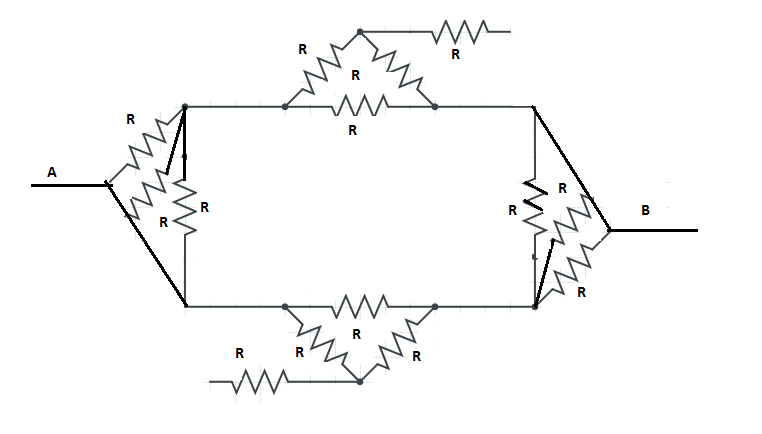
$\begin{align}
  & A.\text{ }R \\
 & B.\text{ }\dfrac{3R}{4} \\
 & C.\text{ }\dfrac{R}{2} \\
 & D.\text{ }2R \\
\end{align}$

Answer 1

Hint: As we know that current only flows in a closed loop of circuit therefore first we will ignore resistance that are not closed loop then after we will simplify the given circuit even further by using the formula for the resistance either connected in parallel or in series which will gives us equivalent resistance of a circuit.

Formula used:
$\begin{align}
  & {{R}_{e}}={{R}_{1}}+{{R}_{2}}+......{{R}_{n}} \\
 & \dfrac{1}{{{R}_{e}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+....\dfrac{1}{{{R}_{n}}} \\
\end{align}$

Complete answer:
As we know those current flows only when the circuit is in closed loop now as we can see that upper and the lower resistance is not in a closed loop therefore we can remove or ignore those two resistances as shown in the figure.

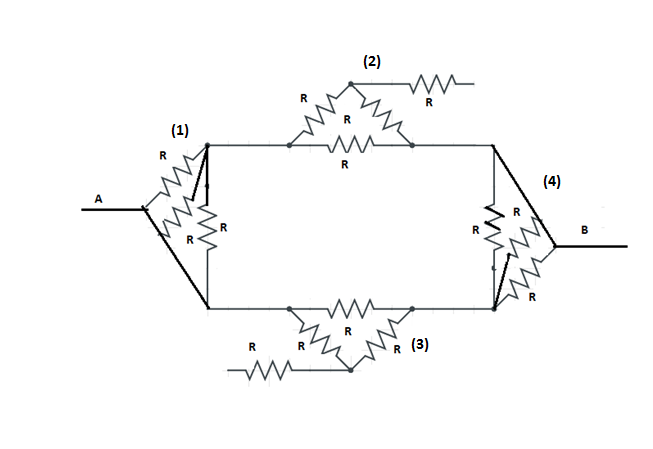
Now as to simplify the circuit we have divided it in 4 parts now for part 2 and 3,

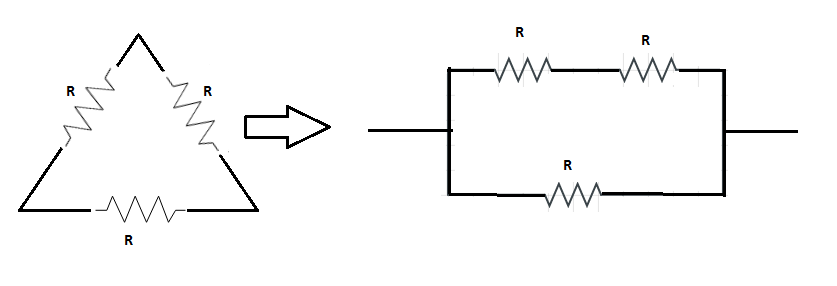
In the triangle circuit two resistors are in the series with each other and both are in parallel with the third resistance,
Now the equivalent resistance is,
$\begin{align}
  & \Rightarrow \dfrac{1}{{{R}_{e}}}=\dfrac{1}{R+R}+\dfrac{1}{R} \\
 & \Rightarrow \dfrac{1}{{{R}_{e}}}=\dfrac{3R}{2{{R}^{2}}} \\
 & \therefore {{R}_{e}}=\dfrac{2}{3}R \\
\end{align}$
Now for the part (1) and the part (4)

As we can see that all the three resistance are in the parallel therefore equivalent resistance is,
$\begin{align}
  & \Rightarrow \dfrac{1}{{{R}_{e}}}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R} \\
 & \Rightarrow \dfrac{1}{{{R}_{e}}}=\dfrac{3}{R} \\
 & \therefore {{R}_{e}}=\dfrac{R}{3} \\
\end{align}$
Now put all the 4 parts equivalent resistance in the main circuit to simplify the given circuit further.

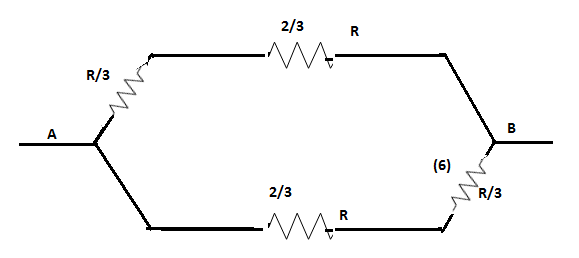
For the part (5) and (6)
$\begin{align}
  & {{R}_{e}}=\dfrac{R}{3}+\dfrac{2}{3}R \\
 & {{R}_{e}}=\dfrac{3R}{3} \\
 & {{R}_{e}}=R \\
\end{align}$
Putting the values of the part (5) and part (6) in a circuit,

Now both resistances are in parallel with each other.
$\begin{align}
  & \Rightarrow \dfrac{1}{{{R}_{e}}}=\dfrac{1}{R}+\dfrac{1}{R} \\
 & \Rightarrow \dfrac{1}{{{R}_{e}}}=\dfrac{2}{R} \\
 & \therefore {{R}_{e}}=\dfrac{R}{2} \\
\end{align}$

Therefore correct option is (C) $\dfrac{R}{2}$ .

Note:
As an approach to solve this question first we remove two resistances that are not in a closed loop then we divide circuit in 4 parts and find their equivalent resistance to simplify the circuit and by putting values of 4 parts we again divided circuit in 2 parts and find equivalent resistance of them finally we got equivalent resistance between A and B.