Question

Find the equation of the perpendicular bisector of a straight line segment joining the points$(3,4)$,$(-1,2)$.

Answer 1

Hint: Name the points and perpendicular bisector. Find the midpoint and slope of $(3,4)$ and $(-1,2)$. Put ${{m}_{1}}{{m}_{2}}=-1$ and you will get the slope of the perpendicular bisector. After that use slope point form and you will get the equation.

A perpendicular bisector can be defined as a line segment that intersects another line perpendicularly and divides it into two equal parts.
Two lines are said to be perpendicular to each other when they intersect in such a way that they form $90{}^\circ $ with each other. And, a bisector divides a line into two equal halves.
Thus, a perpendicular bisector of a line segment $AB$ implies that it intersects $AB$ at $90{}^\circ $ and cuts it into two halves.
Properties of a Perpendicular Bisector
1) It divides $AB$ into two equal halves or bisects it.
2) It makes right angles with (or is perpendicular to) $AB$.
3) Every point in the perpendicular bisector is equidistant from point $A$ and $B$.
While working with practical geometry, you will often find the application of perpendicular bisectors; say when you are asked to draw an isosceles triangle, or when you have to determine the center of a circle, etc.

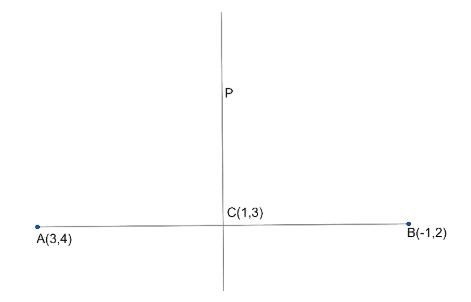
So in question, there are two points, so let us consider the points as $A(3,4)$ and $B(-1,2)$.
So $AB$ is the segment and we want to find the equation of perpendicular bisector i.e. to find the equation of line $P$ perpendicular to the segment $AB$.
So as it is a perpendicular bisector, so the point $C$ is the midpoint of the segment $AB$.
So point $C$ should be $(a,b)$, from which line $P$ passes.
So the point $C$ is the midpoint of the segment $AB$.
$(a,b)=\left( \dfrac{3+(-1)}{2},\dfrac{4+2}{2} \right)=\left( 1,3 \right)$
So we get a point $C(1,3)$.
Now we have to find the slope of the line $P$.
For that, we should find the slope of the segment $AB$.
So let${{m}_{1}}$ be the slope of the segment $AB$.
${{m}_{1}}=\dfrac{2-4}{-1-3}=\dfrac{-2}{-4}=\dfrac{1}{2}$
So ${{m}_{1}}=\dfrac{1}{2}$,
Now we know if a line is perpendicular to segment, so the product of their slopes is equal to $-1$.
So let slope of the line $P$ be ${{m}_{2}}$.
So we get,
${{m}_{1}}{{m}_{2}}=-1$
$\dfrac{1}{2}{{m}_{2}}=-1$
So we get ${{m}_{2}}$.
${{m}_{2}}=-2$,
So we have got the slope of a line $P$and also know that it is the perpendicular bisector of the line segment $AB$.
So it passes through the point $C$.
So now we have a slope and a point so we can use the slope point form to find the equation of the perpendicular bisector.
So general form of slope point form is, if the point is $({{x}_{1}},{{y}_{1}})$ from which the line passes, and its slope $m=-2$, then, the line is given by :
$y-{{y}_{1}}=m(x-{{x}_{1}})$
So substituting for $m,{{x}_{1}},{{y}_{1}}$, we get,
$y-3=\left( -2 \right)(x-1)$
So simplifying in a simple manner we get,
$\begin{align}
  & y-3=-2x+2 \\
 & 2x+y=5 \\
\end{align}$
So we get the equation of perpendicular bisector i.e. line $P$ of the straight line segment joining the points $(3,4)$,$(-1,2)$ is $2x+y=5$.

Note: Read the question carefully. Be familiar with the properties. Don’t confuse yourself with ${{m}_{1}}{{m}_{2}}=-1$ this one. Also, you should know the general form of slope point form $y-{{y}_{1}}=m(x-{{x}_{1}})$. While substituting do not confuse with the points. Also while finding the slope be careful of the substitutions.