Question

Find the equation of the line in vector form which passes through \[\left( {1,2,3} \right)\] and parallel to the vector \[3\widehat i + 2\widehat j - 2\widehat k\].

Answer 1

Hint: Here in this question, we have to find the vector equation of a line passing through a point with position vector \[\overrightarrow a \] and parallel to a vector \[\overrightarrow b \]using a equation \[\overrightarrow r = \overrightarrow a + \lambda \overrightarrow b \], where \[\overrightarrow a \] is the line passes through \[\left( {1,2,3} \right)\] so \[\overrightarrow a = 1\widehat i + 2\widehat j + 3\widehat k\] and \[\overrightarrow b = 3\widehat i + 2\widehat j - 2\widehat k\] , on substituting we get the required solution.

Complete step-by-step answer:
Let \[\overrightarrow a \] be the position vector of the given point A with respect to the origin O of the rectangular coordinate system. Let \[l\] be the line which passes through the point A and is parallel to a given vector \[\overrightarrow b \]. Let \[\overrightarrow r \] be the position vector of an arbitrary point P on the line.

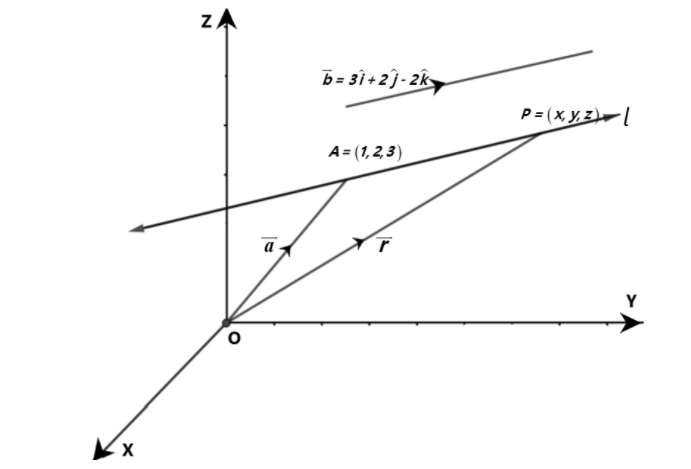
Here, \[\overrightarrow {AP} \] is parallel to the vector \[\overrightarrow b \], i.e., \[\overrightarrow {AP} = \lambda \overrightarrow b \], where \[\lambda \] is some real number.
But
\[\overrightarrow {AP} = \overrightarrow {OP} - \overrightarrow {OA} \]
\[\lambda \overrightarrow b = \overrightarrow r - \overrightarrow a \]
Hence, the vector equation of the line is given by \[\overrightarrow r = \overrightarrow a + \lambda \overrightarrow b \]-----(1)
Given, the line passes through \[\left( {1,2,3} \right)\], so the position vector \[\overrightarrow a = 1\widehat i + 2\widehat j + 3\widehat k\] and parallel to the vector \[3\widehat i + 2\widehat j - 2\widehat k\].
Now, putting value of \[\overrightarrow a \] and \[\overrightarrow b \] in equation (1), we have
\[\therefore \,\,\,\overrightarrow r = \left( {1\widehat i + 2\widehat j + 3\widehat k} \right) + \lambda \left( {3\widehat i + 2\widehat j - 2\widehat k} \right)\]
Hence, the above equation is a vector equation of line which passes through \[\left( {1,2,3} \right)\] and parallel to the vector \[3\widehat i + 2\widehat j - 2\widehat k\].
So, the correct answer is “Option B”.

Note: Remember, the above solved equation is in vector form and one more form of equation i.e., cartesian form of a line passing through the point \[\left( {{x_1},{y_1},{z_1}} \right)\] and parallel to the vector \[a\widehat i + b\widehat j + c\widehat k\] is given as \[\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = \dfrac{{z - {z_1}}}{c}\].
The cartesian form of equation of given question is
Where, \[\left( {{x_1},{y_1},{z_1}} \right) = \left( {1,2,3} \right)\] and \[a\widehat i + b\widehat j + c\widehat k = 3\widehat i + 2\widehat j - 2\widehat k\] i.e., a=3, b=2, c=-2
Then by formula we can written the cartesian equation as:
 \[\dfrac{{x - 1}}{3} = \dfrac{{y - 2}}{2} = \dfrac{{z - 3}}{{ - 2}}\].