Question

Find the equation of the circle circumscribing a square ABCD with side l and AB and AD as coordinate axes.

Answer 1

Hint: Here we will first construct the diagram according to the given information and then find the center and the radius of the circle.
Also, the equation of the circle is given by:-
\[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}\]

where (a, b) is the center of the circle and r is the radius of the circle.

Complete step-by-step answer:
Let us first construct the diagram according to the given information:
                    

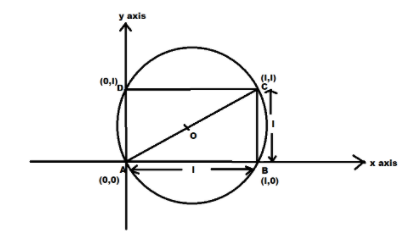
where ABCD is a square with side l and AB and AD as coordinate axes.

Now we will calculate the coordinate of the center of the circle and also the length of its radius.

Since we are given that ABCD is a square and AB and CD are coordinate axes and also the length of the side of the square is l
Therefore,
The coordinates of the vertices of the square are given by:-
\[
  A(0,0) \\
  B(l,0) \\
  C(l,l) \\
  D(0,l) \\
 \]

Now since we know that the diagonal of the square is given by:-
\[diagonal = \sqrt 2 \times side\]
Therefore, diagonal AC is given by:-
\[
  AC = \sqrt 2 \times l \\
   \Rightarrow AC = \sqrt 2 l \\
 \]
Where l is the length of the side of the square.

Also we know that since O is the midpoint of AC
Therefore,
\[OA = OC = \dfrac{1}{2}AC\]
Where OA or OC is the radius of the circle.
Hence putting in the value we get:-

\[
  OA = OC = \dfrac{1}{2}\sqrt 2 l \\
   \Rightarrow r = OA = OC = \dfrac{l}{{\sqrt 2 }} \\
 \]
Therefore the radius r of the circle is \[\dfrac{l}{{\sqrt 2 }}\]


Now let O be the center of the circle with coordinates (a, b) and it is the midpoint of AC
Therefore, we will calculate the coordinates of O using the midpoint formula.
The midpoint (a, b) for two points \[\left( {x_1, y_1} \right)\] and \[\left( {x_2, y_2} \right)\]is given by:-
\[a = \dfrac{{x_1 + x_2}}{2};b = \dfrac{{y_1 + y_2}}{2}\]
Here,
\[
  \left( {x_1,y_1} \right) = A\left( {0,0} \right) \\
   \Rightarrow \left( {x_1,y_1} \right) = \left( {0,0} \right) \\
  \left( {x_2,y_2} \right) = C\left( {l,l} \right) \\
   \Rightarrow \left( {x_2,y_2} \right) = \left( {l,l} \right) \\
 \]
Hence applying the midpoint formula and evaluating the coordinates of O we get:-
\[
  a = \dfrac{{0 + l}}{2} \\
   \Rightarrow a = \dfrac{l}{2} \\
  b = \dfrac{{0 + l}}{2} \\
   \Rightarrow b = \dfrac{l}{2} \\
 \]
Hence the coordinates of the center of the circle are:
\[\left( {a,b} \right) = \left( {\dfrac{l}{2},\dfrac{l}{2}} \right)\]
Now since we know that the equation of the circle is given by:-
\[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}\]

Where (a, b) is the center of the circle and r is the radius of the circle.
Hence putting in the respective values we get:-
\[
  {\left( {x - \dfrac{l}{2}} \right)^2} + {\left( {y - \dfrac{l}{2}} \right)^2} = {\left( {\dfrac{l}{{\sqrt 2 }}} \right)^2} \\
  {\left( {x - \dfrac{l}{2}} \right)^2} + {\left( {y - \dfrac{l}{2}} \right)^2} = \dfrac{{{l^2}}}{2} \\
 \]

Hence the equation of the circle is:-
\[{\left( {x - \dfrac{l}{2}} \right)^2} + {\left( {y - \dfrac{l}{2}} \right)^2} = \dfrac{{{l^2}}}{2}\]

Note: Students should note that the radius of the circle is half the length of the diameter of the circle.
Also, all the sides of a square are equal.
Here students may make mistakes while calculating the coordinates of the vertices of the square so the coordinates should be observed and calculated wisely.