Questions & Answers
Question
AnswersFind the distances between the following pair of points $(a,0) $and$(0,b)$.
Answer
Verified149.7k+ views
Hint: Use distance formula. Use$({{x}_{1}},{{y}_{1}})\equiv (a,0)$ and $({{x}_{2}},{{y}_{2}})\equiv (0,b)$. So substitute the points you will get the answer.
So about distance,
Distance is the total movement of an object without any regard to direction. We can define
distance as to how much ground an object has covered despite its starting or ending point.
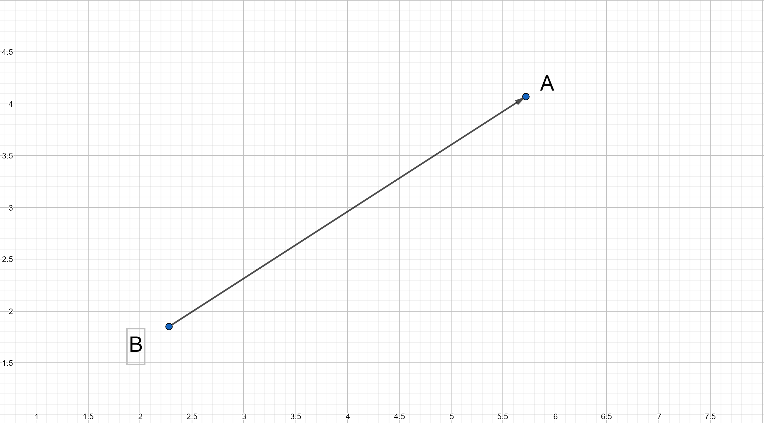
So let $A$ and $B$ be the points on a graph above.
So we have to find the distance between these points $AB$.
We can run lines down from $A$, and along from $B$, to make a Right Angled Triangle.
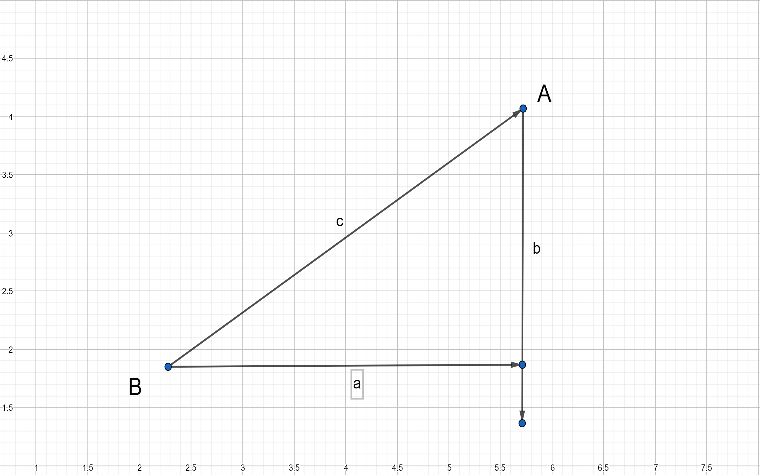
And with a little help from Pythagoras we know that,
${{a}^{2}}+{{b}^{2}}={{c}^{2}}$
So we get,
By simplifying,
$c=\sqrt{{{a}^{2}}+{{b}^{2}}}$…………. (1)
Now let the coordinates of $A({{x}_{1}},{{y}_{1}})$ and $B({{x}_{2}},{{y}_{2}})$
${{x}_{1}}$ means the $x$ coordinate of point $A$ and ${{y}_{1}}$ means the $y$ coordinate
of point $A$,
${{x}_{2}}$ means the $x$ coordinate of point $B$ and ${{y}_{2}}$ means the $y$ coordinate
of point $B$,
So the horizontal distance $a$ is $({{x}_{1}}-{{x}_{2}})$,
Also the vertical distance $b$ is $({{y}_{1}}-{{y}_{2}})$.
Now we can solve for $c$ (the distance between the points),
So from (1), Substituting the value of $a$ and $b$,
We get,
$c=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}$
So we can write$c$ as $dist.(AB)$,
So we get,
$dist.(AB)=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}$
This formula finds the length of a line that stretches between two points: Point $A$ and Point $B$. The linear distance is the square root of the square of the horizontal distance plus
the square of the vertical distance between two points
So the above we get the distance.
So the above formula is a distance formula.
So now we have to find the distance between two points i.e.$(a,0)$ and $(0,b)$,
So let$ A(a,0)$ and $B(0,b)$,
So here ${{x}_{1}}=a,{{x}_{2}}=0,{{y}_{1}}=0 $and \[{{y}_{2}}=b\],
So Using distance formula, we get,
$dist.(AB)=\sqrt{{{(a-0)}^{2}}+{{(0-b)}^{2}}}$
So simplifying in simple manner we get,
$dist.(AB)=\sqrt{{{a}^{2}}+{{b}^{2}}}$
So we get the final distance between the points$(a,0)$and$(0,b)$as$\sqrt{{{a}^{2}}+{{b}^{2}}}$.
Note: So be familiar with the distance formula i.e. $dist.(AB)=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}$. So if the question is
asked to find the distance so first equate the points with$A({{x}_{1}},{{y}_{1}})$ and $B({{x}_{2}},{{y}_{2}})$. Then it will get easy to solve the problem. Otherwise confusion also
occurs between the points. The points get interchange so equate the points to avoid the confusion.
So about distance,
Distance is the total movement of an object without any regard to direction. We can define
distance as to how much ground an object has covered despite its starting or ending point.
So let $A$ and $B$ be the points on a graph above.
So we have to find the distance between these points $AB$.
We can run lines down from $A$, and along from $B$, to make a Right Angled Triangle.
And with a little help from Pythagoras we know that,
${{a}^{2}}+{{b}^{2}}={{c}^{2}}$
So we get,
By simplifying,
$c=\sqrt{{{a}^{2}}+{{b}^{2}}}$…………. (1)
Now let the coordinates of $A({{x}_{1}},{{y}_{1}})$ and $B({{x}_{2}},{{y}_{2}})$
${{x}_{1}}$ means the $x$ coordinate of point $A$ and ${{y}_{1}}$ means the $y$ coordinate
of point $A$,
${{x}_{2}}$ means the $x$ coordinate of point $B$ and ${{y}_{2}}$ means the $y$ coordinate
of point $B$,
So the horizontal distance $a$ is $({{x}_{1}}-{{x}_{2}})$,
Also the vertical distance $b$ is $({{y}_{1}}-{{y}_{2}})$.
Now we can solve for $c$ (the distance between the points),
So from (1), Substituting the value of $a$ and $b$,
We get,
$c=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}$
So we can write$c$ as $dist.(AB)$,
So we get,
$dist.(AB)=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}$
This formula finds the length of a line that stretches between two points: Point $A$ and Point $B$. The linear distance is the square root of the square of the horizontal distance plus
the square of the vertical distance between two points
So the above we get the distance.
So the above formula is a distance formula.
So now we have to find the distance between two points i.e.$(a,0)$ and $(0,b)$,
So let$ A(a,0)$ and $B(0,b)$,
So here ${{x}_{1}}=a,{{x}_{2}}=0,{{y}_{1}}=0 $and \[{{y}_{2}}=b\],
So Using distance formula, we get,
$dist.(AB)=\sqrt{{{(a-0)}^{2}}+{{(0-b)}^{2}}}$
So simplifying in simple manner we get,
$dist.(AB)=\sqrt{{{a}^{2}}+{{b}^{2}}}$
So we get the final distance between the points$(a,0)$and$(0,b)$as$\sqrt{{{a}^{2}}+{{b}^{2}}}$.
Note: So be familiar with the distance formula i.e. $dist.(AB)=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}$. So if the question is
asked to find the distance so first equate the points with$A({{x}_{1}},{{y}_{1}})$ and $B({{x}_{2}},{{y}_{2}})$. Then it will get easy to solve the problem. Otherwise confusion also
occurs between the points. The points get interchange so equate the points to avoid the confusion.
Students Also Read