Question

How do you find the critical numbers of an absolute value equation $f\left( x \right)=\left| x+3 \right|-1$ ?

Answer 1

Hint: We are given an absolute value in this problem. The parent function of this given absolute value function is $\left| x \right|$, that is, $\left| x+3 \right|$ has been modified from $\left| x \right|$. Therefore, we shall plot the graph of the given function by making changes to the graph of $\left| x \right|$ and then we will locate our critical points of the given function.

Complete step-by-step solution:
This is a linear equation with an absolute value function in one variable. In order to solve this, we must have prior knowledge about solving the absolute value functions as well as about the critical numbers of any function.
The critical point of any function is the point where the function changes its direction. It also indicates the maxima and minima of the function according to the direction in which the graph is changing.
We shall first plot the graph of $f\left( x \right)=\left| x \right|$.

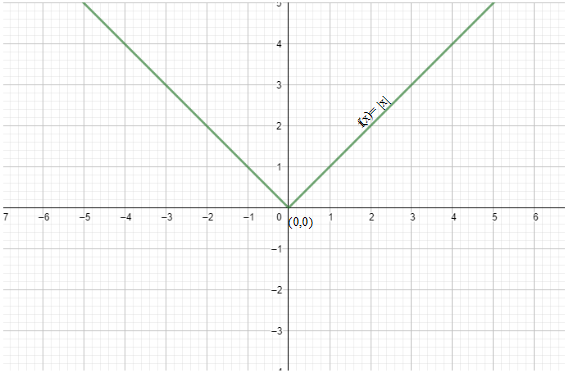
But we have $\left| x+3 \right|$ instead. Thus, we will shift the graph to 3 places to the left of the x-axis, that is on $x=-3$.

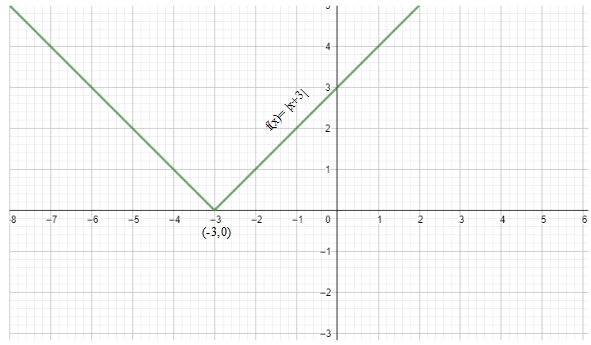
The entire function that we are given is $f\left( x \right)=\left| x+3 \right|-1$. Thus, we will shift the graph 1 place downwards towards the negative y-axis.
Finally, we get our graph of $f\left( x \right)=\left| x+3 \right|-1$ as given below.

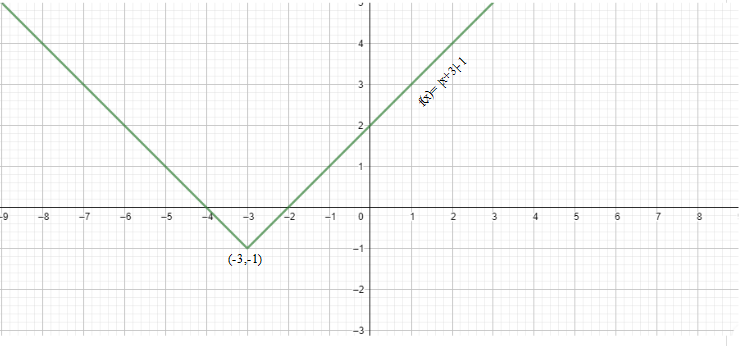
We can observe that the graph is changing its direction at only one point, that is, $\left( -3,-1 \right)$.
Therefore, the critical numbers of an absolute value equation $f\left( x \right)=\left| x+3 \right|-1$ is $x=-3$ and $y=-1$.

Note: Usually, critical points are calculated by differentiating the function once and then equating that differential with zero. The values of x and then consequently y, that we shall obtain by doing so would be called the critical point(s) of the function. However, for some functions, the critical points can be easily determined from their graphs.