Question

Find the centroid of a triangle, mid-points of whose sides are\[\left( {1,2,3} \right)\], \[\left( {3,0,1} \right)\]and\[\left( { - 1,1, - 4} \right)\].
A.\[\left( { - 1, - 1, - 2} \right)\]
B.\[\left( { - 1,2, - 2} \right)\]
C.\[\left( { - 1,1, - 2} \right)\]
D.\[\left( {1,1, - 2} \right)\]

Answer 1

Hint: The centroid of a triangle is the intersection of the medians of the triangle; it is basically the geometric center of a plane figure. It is always located at the interior of the triangles.
Here, in the question we need to determine the centroid of the triangle whose vertices are given. Add the value of each axis of the three vertices and divide them with three and repeat this for the other two axes to find the centroid. To find the median of a side, add the vertices of each axis of that line segment and divide them by 2 and repeat this for the other axis.


Complete step by step solution:
Let the centroid of the triangle be G
Given the vertices of the triangle
\[A\left( {{x_1},{y_1},{z_1}} \right) \to \left( {1,2, - 3} \right)\]
\[B\left( {{x_2},{y_2},{z_2}} \right) \to \left( {3,0,1} \right)\]
\[C\left( {{x_3},{y_3},{z_3}} \right) \to \left( { - 1,1, - 4} \right)\]

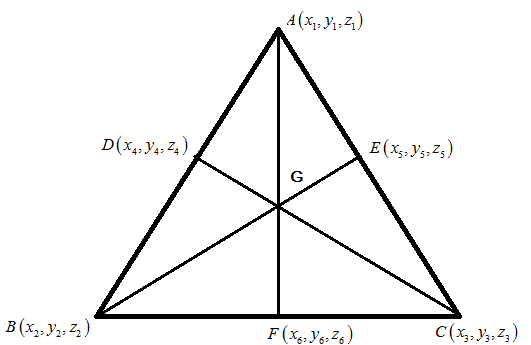
Let the midpoint of the sides of the triangle be D, E, F, hence the midpoint of the triangle will be,
For side AB
\[D\left( {{x_4},{y_4},{z_4}} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2},\dfrac{{{z_1} + {z_2}}}{2}} \right)\]
For side AC
\[E\left( {{x_5},{y_5},{z_5}} \right) = \left( {\dfrac{{{x_1} + {x_3}}}{2},\dfrac{{{y_1} + {y_3}}}{2},\dfrac{{{z_1} + {z_3}}}{2}} \right)\]
For side AC
\[F\left( {{x_6},{y_6},{z_6}} \right) = \left( {\dfrac{{{x_2} + {x_3}}}{2},\dfrac{{{y_2} + {y_3}}}{2},\dfrac{{{z_2} + {z_3}}}{2}} \right)\]
We know the centroid of a triangle is given by the formula
\[G = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right)\]
Where the given coordinates are
\[A\left( {{x_1},{y_1},{z_1}} \right) \to \left( {1,2, - 3} \right)\]
\[B\left( {{x_2},{y_2},{z_2}} \right) \to \left( {3,0,1} \right)\]
\[C\left( {{x_3},{y_3},{z_3}} \right) \to \left( { - 1,1, - 4} \right)\]
Hence we can calculate the centroid
\[
  G = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right) \\
   = \left( {\dfrac{{1 + 3 - 1}}{3},\dfrac{{2 + 0 + 1}}{3},\dfrac{{ - 3 + 1 - 4}}{3}} \right) \\
   = \left( {\dfrac{3}{3},\dfrac{3}{3},\dfrac{{ - 6}}{3}} \right) \\
   = \left( {1,1, - 2} \right) \\
 \]
Hence the centroid of the triangle is \[G = \left( {1,1, - 2} \right)\]
Option (D) is correct.


Note: The midpoint is the middle point of a line segment, and it is equidistant from both ends of a line segment. Students should be careful while selecting the coordinates for the centroid. Only the respective coordinates should be taken for the corresponding centroid axes.