Question

If two parallel lines are intersected by a transversal, then prove that bisectors of the interior angles form a rectangle.

Answer 1

Hint: First of all, construct a quadrilateral with two parallel lines intersected by a transversal and the bisectors of the interior angles. Then show that the formed quadrilateral is parallelogram and one of its angles is the right angle then the given quadrilateral is a rectangle.

Complete step-by-step answer:
Construction: Two parallel lines AB and CD and a transversal EF intersect them at G and H respectively. GM, HM, GL and HL are the bisectors of the two pairs of interior angles.

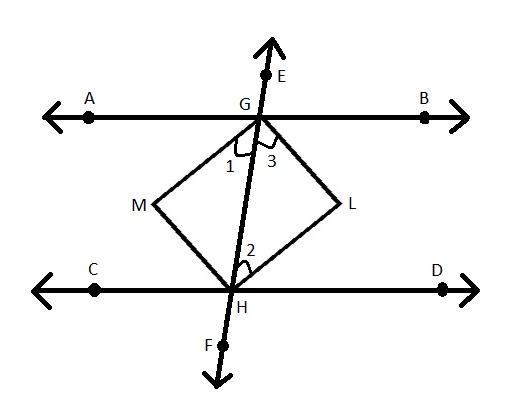
To prove: GHML is a rectangle.
Proof:
Since \[AB\parallel CD\]
\[\angle AGH = \angle DHG{\text{ }}\left( {{\text{Alternate interior angles}}} \right)\]
Dividing both side by 2, we have
\[
   \Rightarrow \dfrac{1}{2}\angle AGH = \dfrac{1}{2}\angle DHG \\
   \Rightarrow \angle 1 = \angle 2{\text{ }}\left( {{\text{GM & HL are bisectors of }}\angle {\text{AGH and }}\angle {\text{DHG respectively}}} \right) \\
   \Rightarrow GM\parallel HL{\text{ }}\left( {\angle 1{\text{ and }}\angle {\text{2 from a pair of alternate interior angles are equal}}} \right) \\
\]
Similarly, \[GL\parallel MH\]
So, GMHL is a parallelogram.
Since \[AB\parallel CD\]
We have \[\angle BGH + \angle DHG = {180^\circ}\] as the sum of interior angles on the same side of the transversal is equal to \[{180^\circ}\].
Dividing both sides by 2, we have
\[
   \Rightarrow \dfrac{1}{2}\angle BGH + \dfrac{1}{2}\angle DHG = {90^\circ} \\
   \Rightarrow \angle 3 + \angle 2 = {90^\circ}........................................................\left( 1 \right) \\
\]
In \[\Delta GLH\] as the sum of the angles is equal to \[{180^\circ}\], we have
\[
   \Rightarrow \angle 2 + \angle 3 + \angle L = {180^\circ} \\
   \Rightarrow {90^\circ} + \angle L = {180^\circ}{\text{ }}\left( {{\text{Using }}\left( 1 \right)} \right) \\
   \Rightarrow \angle L = {180^\circ} - {90^\circ} \\
  \therefore \angle L = {90^\circ} \\
\]
Thus, in a parallelogram GMHL, \[\angle L = {90^\circ}\]
We know that if one of the angles is the right angle in the parallelogram then it is also a rectangle.
Hence, proved that GHML is a rectangle.
Thus, if two parallel lines are intersected by a transversal, then bisectors of the interior angles form a rectangle.

Note: The sum of interior angles on the same side of the transversal is equal to \[{180^\circ}\]. When two lines are crossed by another line which is called as the transversal the alternate interior angles are equal.