Question

How do you find the centre, vertices, foci, and asymptotes of the hyperbola, and sketch its graph of \[\dfrac{{{x}^{2}}}{9}-\dfrac{{{y}^{2}}}{16}=1\]?

Answer 1

Hint: For answering this question we need to find the centre, vertices, foci and asymptotes of the given hyperbola. The general form of hyperbola is \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] for this the centre is given as $\left( 0,0 \right)$ and the vertices are given as $\left( a,0 \right)$ and $\left( -a,0 \right)$ . The distance between the foci and the centre is given as $\sqrt{{{a}^{2}}+{{b}^{2}}}$ and the equations of the asymptotes are given as $y=\dfrac{b}{a}x$ and $y=-\dfrac{b}{a}x$ .

Complete step by step answer:
Now considering from the question we have been given an equation of a hyperbola as follows \[\dfrac{{{x}^{2}}}{9}-\dfrac{{{y}^{2}}}{16}=1\] .
From the basic concepts of hyperbola we know that the general form of hyperbola is \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] for this the centre is given as $\left( 0,0 \right)$ and the vertices are given as $\left( a,0 \right)$ and $\left( -a,0 \right)$ . The distance between the foci and the centre is given as $\sqrt{{{a}^{2}}+{{b}^{2}}}$ and the equations of the asymptotes are given as $y=\dfrac{b}{a}x$ and $y=-\dfrac{b}{a}x$ .
By comparing we can say that $a=3$ and $b=4$ .
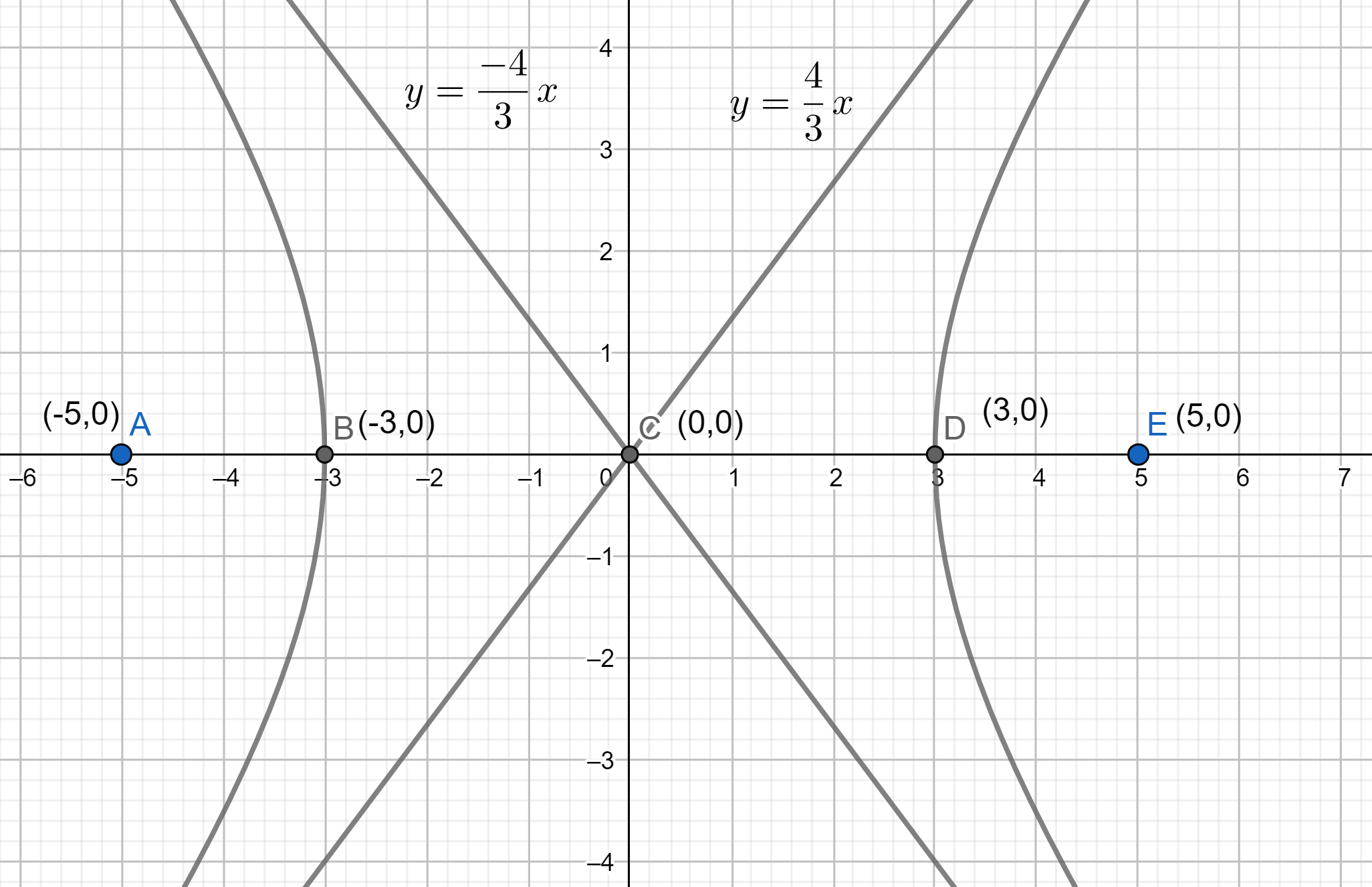
Hence we can conclude that the centre is given as $\left( 0,0 \right)$ and the vertices are given as $\left( a,0 \right)\Rightarrow \left( 3,0 \right)$ and $\left( -a,0 \right)\Rightarrow \left( -3,0 \right)$ . The distance between the foci and the centre is given as $\sqrt{{{a}^{2}}+{{b}^{2}}}\Rightarrow \sqrt{9+16}=\sqrt{25}\Rightarrow 5$ and the equations of the asymptotes are given as $y=\dfrac{b}{a}x\Rightarrow y=\dfrac{4}{3}x$ and $y=-\dfrac{b}{a}x\Rightarrow y=\dfrac{-4}{3}x$ .
As the distance between centre and foci is $5$ the points of the focus will be $\left( 5,0 \right)$ and $\left( -5,0 \right)$ .
By plotting the centre, foci, vertex and the asymptotes and joining them we will have the graph of the hyperbola as shown here-

Note: We should be very careful while comparing the equation of the given hyperbola and general form of the equation of hyperbola. Also, we should do the calculation very carefully while finding the distance from the centre to focus. Also, we should be well known about the general forms of conic sections. Similarly for a parabola ${{x}^{2}}=4ay$ the vertex is given as $(0,0)$ and the focus is given as $\left( a,0 \right)$