Question

Find the area of the region bounded by the curve $xy={{c}^{2}}$ the x-axis and the lines x = c, x = 2c.

Answer 1

Hint: In this question, we are given four equations and we have to find the area between them. Here, first we will try to draw a rough diagram for understanding the region. After that, we will apply a definite integral for finding the area of the region. We will evaluate limits and functions that will be used in the definite integral using diagrams.

Complete step by step answer:
Let us first draw a diagram for the given equations.
For $xy={{c}^{2}}$ as we can see that by putting x = 0 or y = 0, we seek that value does not exist, hence, the curve does not intersect x-axis or y-axis. Now, let us find points where this curve meets x = c and x = 2c.
For x = 2c, putting in $xy={{c}^{2}}$ we get:
\[\begin{align}
  & 2cy={{c}^{2}} \\
 & \Rightarrow y=\dfrac{c}{2} \\
\end{align}\]
Hence, point of intersection of x = 2c and $xy={{c}^{2}}$ is $\left( 2c,\dfrac{c}{2} \right)$
For x = c, putting in $xy={{c}^{2}}$ we get:
\[\begin{align}
  & cy={{c}^{2}} \\
 & \Rightarrow y=c \\
\end{align}\]
Hence, the point of intersection of x = c and $xy={{c}^{2}}$ is (c, c).
According to information and points found above, diagram becomes

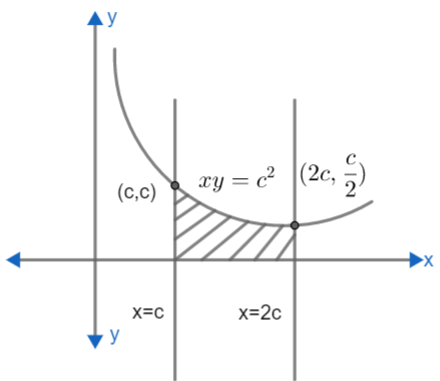
For the region between the x axis, x = c, x = 2c and $xy={{c}^{2}}$. We can use definite integration because we know that region under any curve is evaluated using definite integral $\int\limits_{a}^{b}{f\left( x \right)}dx$ where f(x) represents curve under which integral is to be found, a and b are the points of x axis between which we have to find region. From diagram we can see that, curve $xy={{c}^{2}}$ will represent f(x) = y which is given as $f\left( x \right)\div \dfrac{{{c}^{2}}}{x}$. Also 'a' becomes 'c' and the integral $\int\limits_{c}^{2c}{\dfrac{{{c}^{2}}}{x}}dx$ to find area bounded by curves $xy={{c}^{2}}$, x = c, x = 2c and x-axis.
\[\text{Area}=\int\limits_{c}^{2c}{\dfrac{{{c}^{2}}}{x}}dx={{c}^{2}}\int\limits_{c}^{2c}{\dfrac{1}{x}}dx\]
As we know $\int{\dfrac{1}{x}}dx=\ln \left( x \right)+c$
Therefore, $F\left( x \right)=\ln \left( x \right)$ for $f\left( x \right)=\dfrac{1}{x}$
By fundamental theorem of calculus,
\[\int\limits_{a}^{b}{f\left( x \right)}dx=F\left( b \right)-F\left( a \right)\]
Where, F(x) is the integration of f(x).
\[\text{Area}={{c}^{2}}\int\limits_{c}^{2c}{\dfrac{1}{x}}dx={{c}^{2}}\left( \ln \left( 2c \right)-\ln \left( c \right) \right)\]
As we know $\ln x-\ln y=\ln \left( \dfrac{x}{y} \right)$ hence, area becomes
\[\begin{align}
  & \text{Area}={{c}^{2}}\left( \ln \left( \dfrac{2c}{c} \right) \right) \\
 & \Rightarrow \text{Area}={{c}^{2}}\ln \left( 2 \right) \\
\end{align}\]
Thus, area of region bounded by the curve $xy={{c}^{2}}$ x-axis and lines x = c, x = 2c is ${{c}^{2}}\ln \left( 2 \right)$ where ln is natural log.

Note: Students should take care while drawing diagrams and finding intersection points. Don't forget to convert the equation of curve into function of x only. Here, f(x) simply represents the value of y obtained from the equation of the curve under which area is to be found. Students should remember the basic integration formulas for solving these sums.