
Find the area of the region bounded by the parabola \[y={{x}^{2}}\] and $y=\left| x \right|$?

Answer
588.9k+ views
Hint: We start solving the problem by recalling the concept of finding area through integration. We find the limits of integration and integrand for the area from the plot drawn between the given two functions. We then use the definition of modulus function $\left| x \right|=\left\{ \begin{matrix}
x,\text{ for }x>0 \\
0,\text{ for }x=0 \\
-x,\text{ for }x<0 \\
\end{matrix} \right.$ and $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}+C$, $\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)}=\left[ f\left( x \right) \right]_{a}^{b}=f\left( b \right)-f\left( a \right)$ to find the integration result. We then make subsequent calculations to get the value of required area.
Complete step-by-step solution:
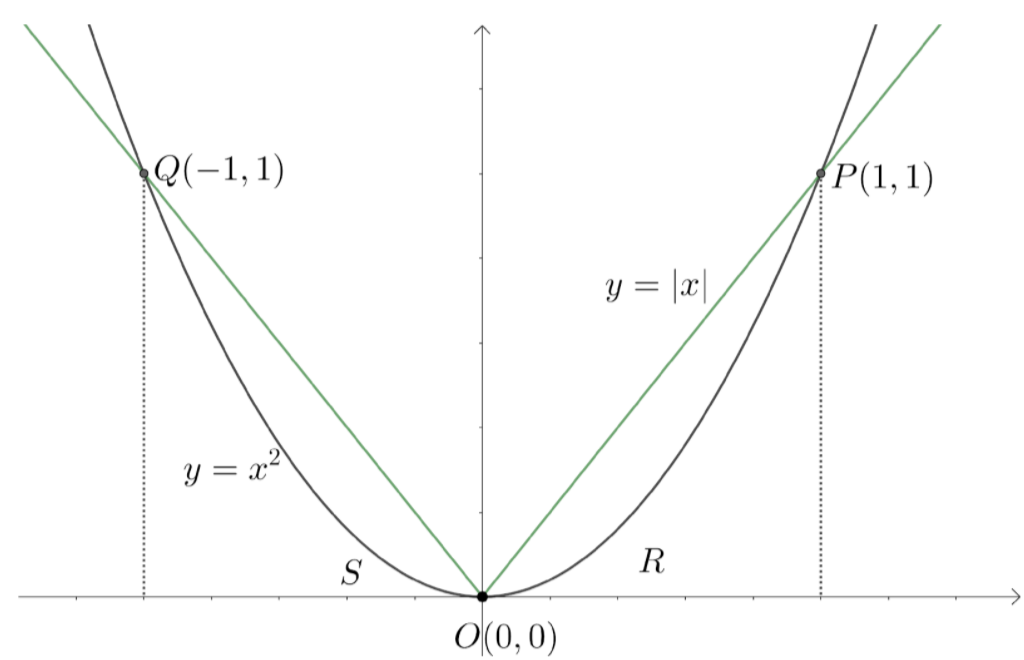
According to the problem, we need to find the area of the region bounded by the parabola \[y={{x}^{2}}\] and the function $y=\left| x \right|$.
We know that the area bounded by the curves will be region where they were making a closed region. From the figure, we can see that the closed region formed by the region is between the points $\left( -1,1 \right)$ to $\left( 0,0 \right)$ and between $\left( 0,0 \right)$ and $\left( 1,1 \right)$.
We know that the area bounded by the curves $f\left( x \right)$, $g\left( x \right)$ between the values $x=a$ and $x=b$is defined by $\int\limits_{a}^{b}{f\left( x \right)-g\left( x \right)dx}$, where $aFrom the figure we can see that the function $y=\left| x \right|$ lies above the parabola \[y={{x}^{2}}\] between $x=-1$ and $x=0$, also between $x=0$ and $x=1$.
So, the area of the region (A) bounded by the parabola \[y={{x}^{2}}\] and the function $y=\left| x \right|$ is,
$\Rightarrow A=\int\limits_{-1}^{0}{\left( \left| x \right|-{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{\left( \left| x \right|-{{x}^{2}} \right)dx}$ ---(1).
We know that the definition of modulus function is defined as $\left| x \right|=\left\{ \begin{matrix}
x,\text{ for }x>0 \\
0,\text{ for }x=0 \\
-x,\text{ for }x<0 \\
\end{matrix} \right.$. We use this in equation (1).
$\Rightarrow A=\int\limits_{-1}^{0}{\left( -x-{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{\left( x-{{x}^{2}} \right)dx}$.
We know that $\int{\left( f\left( x \right)+g\left( x \right) \right)dx}=\int{f\left( x \right)dx}+\int{g\left( x \right)dx}$.
$\Rightarrow A=\int\limits_{-1}^{0}{\left( -x \right)dx}+\int\limits_{0}^{1}{\left( -{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{xdx}+\int\limits_{0}^{1}{\left( -{{x}^{2}} \right)dx}$.
$\Rightarrow A=-\int\limits_{-1}^{0}{xdx}-\int\limits_{0}^{1}{{{x}^{2}}dx}+\int\limits_{0}^{1}{xdx}-\int\limits_{0}^{1}{{{x}^{2}}dx}$.
We know that $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}+C$ and $\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)}=\left[ f\left( x \right) \right]_{a}^{b}=f\left( b \right)-f\left( a \right)$.
$\Rightarrow A=-\left[ \dfrac{{{x}^{2}}}{2} \right]_{-1}^{0}-\left[ \dfrac{{{x}^{3}}}{3} \right]_{-1}^{0}+\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{1}-\left[ \dfrac{{{x}^{3}}}{3} \right]_{0}^{1}$.
$\Rightarrow A=-\left[ \dfrac{{{0}^{2}}}{2}-\dfrac{{{\left( -1 \right)}^{2}}}{2} \right]-\left[ \dfrac{{{0}^{3}}}{3}-\dfrac{{{\left( -1 \right)}^{3}}}{3} \right]+\left[ \dfrac{{{1}^{2}}}{2}-\dfrac{{{0}^{2}}}{2} \right]-\left[ \dfrac{{{1}^{3}}}{3}-\dfrac{{{0}^{3}}}{3} \right]$.
$\Rightarrow A=-\left[ \dfrac{0}{2}-\dfrac{1}{2} \right]-\left[ \dfrac{0}{3}-\left( \dfrac{-1}{3} \right) \right]+\left[ \dfrac{1}{2}-\dfrac{0}{2} \right]-\left[ \dfrac{1}{3}-\dfrac{0}{3} \right]$.
$\Rightarrow A=-\left[ 0-\dfrac{1}{2} \right]-\left[ 0+\dfrac{1}{3} \right]+\left[ \dfrac{1}{2}-0 \right]-\left[ \dfrac{1}{3}-0 \right]$.
$\Rightarrow A=-\left[ -\dfrac{1}{2} \right]-\left[ \dfrac{1}{3} \right]+\left[ \dfrac{1}{2} \right]-\left[ \dfrac{1}{3} \right]$.
$\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{3}$.
$\Rightarrow A=\dfrac{1}{3}$.
So, we have found the area bounded by the parabola \[y={{x}^{2}}\] and the function $y=\left| x \right|$ as $\dfrac{1}{3}$.
∴ The area bounded by the parabola \[y={{x}^{2}}\] and the function $y=\left| x \right|$ is $\dfrac{1}{3}$.
Note: From the figure, we can see that the area bounded in the regions S and R are equal. So, we can find area of one region and multiply it with (2) in order to get the required area of the bounded. Whenever we are asked to find areas of two intersecting functions, we need to find the area of the closed bounded region. If those are not intersecting, limits of integration have to be given in order to get the area bounded between them.
x,\text{ for }x>0 \\
0,\text{ for }x=0 \\
-x,\text{ for }x<0 \\
\end{matrix} \right.$ and $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}+C$, $\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)}=\left[ f\left( x \right) \right]_{a}^{b}=f\left( b \right)-f\left( a \right)$ to find the integration result. We then make subsequent calculations to get the value of required area.
Complete step-by-step solution:
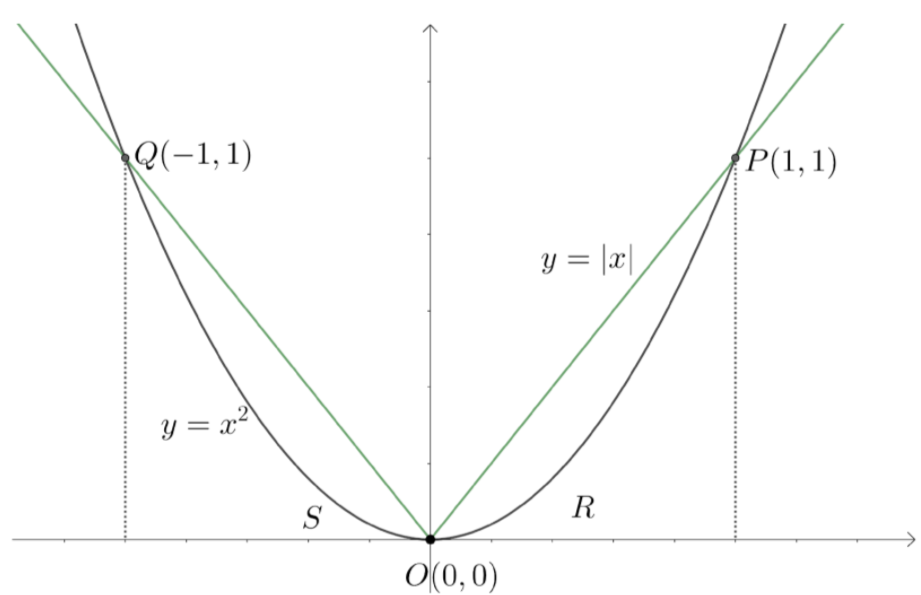
According to the problem, we need to find the area of the region bounded by the parabola \[y={{x}^{2}}\] and the function $y=\left| x \right|$.

We know that the area bounded by the curves will be region where they were making a closed region. From the figure, we can see that the closed region formed by the region is between the points $\left( -1,1 \right)$ to $\left( 0,0 \right)$ and between $\left( 0,0 \right)$ and $\left( 1,1 \right)$.
We know that the area bounded by the curves $f\left( x \right)$, $g\left( x \right)$ between the values $x=a$ and $x=b$is defined by $\int\limits_{a}^{b}{f\left( x \right)-g\left( x \right)dx}$, where $a
So, the area of the region (A) bounded by the parabola \[y={{x}^{2}}\] and the function $y=\left| x \right|$ is,
$\Rightarrow A=\int\limits_{-1}^{0}{\left( \left| x \right|-{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{\left( \left| x \right|-{{x}^{2}} \right)dx}$ ---(1).
We know that the definition of modulus function is defined as $\left| x \right|=\left\{ \begin{matrix}
x,\text{ for }x>0 \\
0,\text{ for }x=0 \\
-x,\text{ for }x<0 \\
\end{matrix} \right.$. We use this in equation (1).
$\Rightarrow A=\int\limits_{-1}^{0}{\left( -x-{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{\left( x-{{x}^{2}} \right)dx}$.
We know that $\int{\left( f\left( x \right)+g\left( x \right) \right)dx}=\int{f\left( x \right)dx}+\int{g\left( x \right)dx}$.
$\Rightarrow A=\int\limits_{-1}^{0}{\left( -x \right)dx}+\int\limits_{0}^{1}{\left( -{{x}^{2}} \right)dx}+\int\limits_{0}^{1}{xdx}+\int\limits_{0}^{1}{\left( -{{x}^{2}} \right)dx}$.
$\Rightarrow A=-\int\limits_{-1}^{0}{xdx}-\int\limits_{0}^{1}{{{x}^{2}}dx}+\int\limits_{0}^{1}{xdx}-\int\limits_{0}^{1}{{{x}^{2}}dx}$.
We know that $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}+C$ and $\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)}=\left[ f\left( x \right) \right]_{a}^{b}=f\left( b \right)-f\left( a \right)$.
$\Rightarrow A=-\left[ \dfrac{{{x}^{2}}}{2} \right]_{-1}^{0}-\left[ \dfrac{{{x}^{3}}}{3} \right]_{-1}^{0}+\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{1}-\left[ \dfrac{{{x}^{3}}}{3} \right]_{0}^{1}$.
$\Rightarrow A=-\left[ \dfrac{{{0}^{2}}}{2}-\dfrac{{{\left( -1 \right)}^{2}}}{2} \right]-\left[ \dfrac{{{0}^{3}}}{3}-\dfrac{{{\left( -1 \right)}^{3}}}{3} \right]+\left[ \dfrac{{{1}^{2}}}{2}-\dfrac{{{0}^{2}}}{2} \right]-\left[ \dfrac{{{1}^{3}}}{3}-\dfrac{{{0}^{3}}}{3} \right]$.
$\Rightarrow A=-\left[ \dfrac{0}{2}-\dfrac{1}{2} \right]-\left[ \dfrac{0}{3}-\left( \dfrac{-1}{3} \right) \right]+\left[ \dfrac{1}{2}-\dfrac{0}{2} \right]-\left[ \dfrac{1}{3}-\dfrac{0}{3} \right]$.
$\Rightarrow A=-\left[ 0-\dfrac{1}{2} \right]-\left[ 0+\dfrac{1}{3} \right]+\left[ \dfrac{1}{2}-0 \right]-\left[ \dfrac{1}{3}-0 \right]$.
$\Rightarrow A=-\left[ -\dfrac{1}{2} \right]-\left[ \dfrac{1}{3} \right]+\left[ \dfrac{1}{2} \right]-\left[ \dfrac{1}{3} \right]$.
$\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{3}$.
$\Rightarrow A=\dfrac{1}{3}$.
So, we have found the area bounded by the parabola \[y={{x}^{2}}\] and the function $y=\left| x \right|$ as $\dfrac{1}{3}$.
∴ The area bounded by the parabola \[y={{x}^{2}}\] and the function $y=\left| x \right|$ is $\dfrac{1}{3}$.
Note: From the figure, we can see that the area bounded in the regions S and R are equal. So, we can find area of one region and multiply it with (2) in order to get the required area of the bounded. Whenever we are asked to find areas of two intersecting functions, we need to find the area of the closed bounded region. If those are not intersecting, limits of integration have to be given in order to get the area bounded between them.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What is a transformer Explain the principle construction class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




