Question

Find the area of $\Delta ABC$.

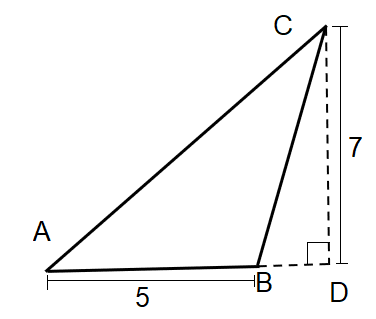
(a) $17.5c{{m}^{2}}$
(b) $16.5c{{m}^{2}}$
(c) $18.5c{{m}^{2}}$
(d) $12c{{m}^{2}}$

Answer 1

Hint: We first form the area of $\Delta ABC$ as $ar\left( \Delta ABC \right)=ar\left( \Delta ACD \right)-ar\left( \Delta BCD \right)$. We take the right-angle triangles and find their areas. We subtract them to find the area of $\Delta ABC$.

Complete step-by-step solution:
The given $\Delta ABC$, has a height of 7 cm.

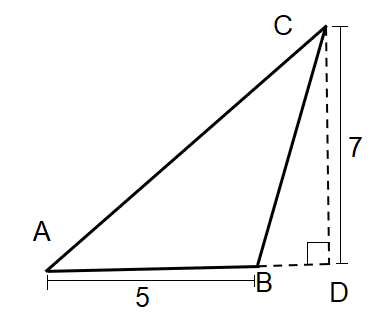
We take the perpendicular point from point C on extended AB as D.
We assume the area of $\Delta ABC$ as $ar\left( \Delta ABC \right)=ar\left( \Delta ACD \right)-ar\left( \Delta BCD \right)$
As the $\angle ADC={{90}^{\circ }}$, therefore we can take both $\Delta ACD$ and $\Delta BCD$ as right-angled triangles.
The height for both of them will be $CD=7$.
Now let us assume the length $BD=a$. Therefore, $AD=AB+BD=5+a$.
Now we find the areas. The formula is half of the multiplication of the sides holding the right-angle.
For $\Delta ACD$, the area is $\dfrac{1}{2}\times AD\times CD=\dfrac{7\left( 5+a \right)}{2}$.
For $\Delta BCD$, the area is $\dfrac{1}{2}\times BD\times CD=\dfrac{7a}{2}$.
So, $ar\left( \Delta ABC \right)=ar\left( \Delta ACD \right)-ar\left( \Delta BCD \right)=\dfrac{7\left( 5+a \right)}{2}-\dfrac{7a}{2}$.
We simplify to get \[ar\left( \Delta ABC \right)=\dfrac{7}{2}\left( 5+a-a \right)=\dfrac{35}{2}=17.5c{{m}^{2}}\].
The correct option is (a).

Note: The height is necessarily needed to be inside the figure. The height on the extended line is also the height of the figure. In that case we can take the area for $\Delta ABC$ as $\dfrac{1}{2}\times AB\times CD=\dfrac{35}{2}$.