Question

Find the area of a rhombus whose side is 6cm and altitude is 4cm. If one of the diagonals is 8cm long, find the length of the other diagonal.

Answer 1

Hint: In this question, first draw the diagram and mark the length of side, altitude and diagonal it will give us a clear picture then use the formula of area of rhombus.

Complete step-by-step answer:

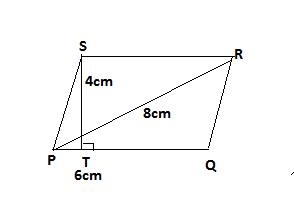
From figure,
Side of Rhombus PQRS, PQ=6cm
Altitude from point S to the side PQ, ST=4cm
We know rhombus is a parallelogram so the area of parallelogram is product of base and altitude.
Now, Area of rhombus \[ = {\text{Base}} \times {\text{height}}\]
$
   \Rightarrow PQ \times ST \\
   \Rightarrow 6 \times 4 \\
   \Rightarrow 24c{m^2} \\
 $
 So, the area of a rhombus is 24cm²
Now, in the question given length of one diagonal, $PR = {d_1} = 8cm$ .
To find the length of another diagonal we use the area of the rhombus.
Area of rhombus $ = \dfrac{{{\text{product of diagonals}}}}{2} = \dfrac{{{d_1} \times {d_2}}}{2}$
We already calculate the area of the rhombus so put the value of area in the above formula.
$
   \Rightarrow 24 = \dfrac{{{d_1} \times {d_2}}}{2} \\
   \Rightarrow 48 = 8 \times {d_2} \\
   \Rightarrow {d_2} = 6cm \\
$
The length of the other diagonal, $SQ = {d_2} = 6cm$ .
So, the area of the rhombus is 24cm² and the length of the other diagonal is 6cm.
Note: Whenever we face such types of problems we use some important points. We use the area of rhombus in two different ways. If we need area we use area of parallelogram but if we need diagonals so we use that formula of area in which diagonals present.