Question

Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.

Answer 1

Hint: First, draw the figure of this question with the help of the information that is given in this question. We will find that there are two triangles in the figure. One of them is an isosceles triangle of which we can find the area. If we carefully notice the other triangle, we will see that the sides of this triangle are a pythagorean triplet. Hence this triangle is a right angle triangle of which we can easily find the area.

Complete step-by-step answer:
Before proceeding with the question, we must know the concept that will be required to solve this question.
In a triangle having sides a, b, c, if we get a relation between the sides of this triangle as,
$c=\sqrt{{{a}^{2}}+{{b}^{2}}}$ , we can say that the triangle is a right angle triangle side with length c as hypotenuse and the other two sides as base and perpendicular. Also, the sides (a, b, c) are called as pythagorean triplet.
For a triangle, the area is equal to $\dfrac{1}{2}$ (base)(height) $.................\left( 1 \right)$.
In the question, we are given a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm and we are required to find the area of this quadrilateral.
Let us first draw the figure of this question with the help of information given.

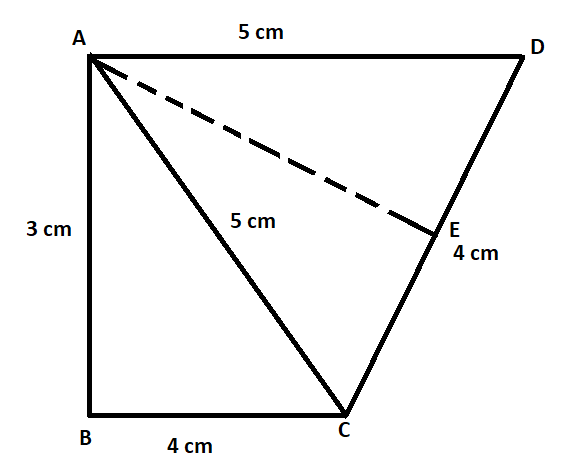
From the figure, we can see that this quadrilateral consists of two triangles ABC and ACD. The sum of the area of these two triangles will give us the area of the quadrilateral ABCD.
In triangle ABC, the three sides are 3cm, 4cm and 5cm. If we carefully notice, we can see that,
$5=\sqrt{{{3}^{2}}+{{4}^{2}}}$
So, we can say that (3, 4, 5) are pythagorean triplet and hence we can say that ABC is a right angle triangle with base BC = 4 cm, height AB = 3 cm and hypotenuse AC = 5 cm.
Using formula $\left( 1 \right)$, the area of triangle ABC is equal to $\dfrac{1}{2}\left( 3 \right)\left( 4 \right)=6c{{m}^{2}}............\left( 2 \right)$.
In triangle ACD, we can see that side AC = side AD. So, this is an isosceles triangle. Let us draw a perpendicular AE on the CD. In the isosceles triangle, perpendicular to the non-equal side bisects the non–equal side. Hence, we can say in triangle ACD, CE = DE = 2 cm.
To find the area of this triangle, we have to find the perpendicular AE. To find the perpendicular AE, we will use Pythagoras theorem.

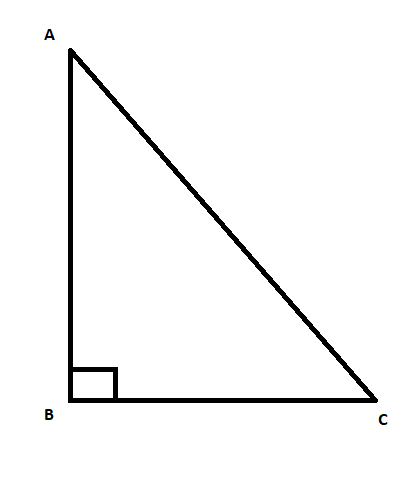
The Pythagoras theorem states that for a right angle triangle, the relation between the sides is given by,
$A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$
Using Pythagoras theorem in triangle ACE, we get,
$\begin{align}
  & A{{C}^{2}}=A{{E}^{2}}+C{{E}^{2}} \\
 & \Rightarrow {{5}^{2}}=A{{E}^{2}}+{{2}^{2}} \\
 & \Rightarrow A{{E}^{2}}=25-4 \\
 & \Rightarrow AE=\sqrt{21} \\
\end{align}$
Using formula $\left( 1 \right)$, the area of the triangle ACD is equal to $\dfrac{1}{2}\left( 4 \right)\left( \sqrt{21} \right)=2\sqrt{21}c{{m}^{2}}............\left( 3 \right)$
The area of quadrilateral ABCD is equal to the sum of the area of the two triangles. So, from $\left( 2 \right)$ and $\left( 3 \right)$, we get,
Area of the quadrilateral = $6+2\sqrt{21}$.
Hence, the answer is $6+2\sqrt{21}$.

Note: There area of triangle ACD can also be found by first finding the area of triangle ACE and then multiplying it by 2 because the perpendicular of an isosceles triangle divides it into two equal parts.