Question

Find the area of a chalk box whose length, breadth and height are $8cm,\,4cm\,and\,2cm$ respectively.

Answer 1

Hint: A cuboid is a 3D shape. Cuboids have six faces, which form a convex polyhedron. Broadly, the faces of the cuboid can be any quadrilateral. More narrowly, rectangular cuboids are made from 6 rectangles, which are placed at right angles. A cuboid that uses all square faces is a cube.
As we know that
$\therefore A = 2(lb + bh + hl)$
Here
l=length
b=breadth
h=height

Complete step-by-step solution:
Given,

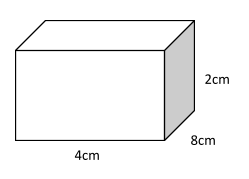
Length of chalk box, $l = 8cm$
Breadth of chalk box, $b = 4cm$
Height of chalk box, $h = 2cm$
Now the area of chalk box,
As we know that
$\therefore A = 2(lb + bh + hl)$
Put the value in equation
\[ \Rightarrow A = 2(8 \times 4 + 4 \times 2 + 2 \times 8)\]
Simplify
$ \Rightarrow A = 2 \times 56$
$ \Rightarrow A = 112c{m^2}$
Hence the area of the chalk box are $112c{m^2}$

Note: All cuboids have these properties- Three dimensions of width, length and depth (or height). Six rectangular faces. All vertices are $90^\circ$. These three properties mean opposite sides of the cuboid are parallel and congruent to each other. The edges of a cuboid meet each other at vertices.