Answer
Verified432.6k+ views
Hint: Here in this we have to find the area between the loop of \[r = 1 + 2\cos \theta \]. To find the area we use formula \[A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r)}^2}d\theta } \], where \[\alpha \]and \[\beta \] are the limit points. Hence by substituting all the values in the formula and then by simplifying we obtain the area of one petal.
Complete step by step explanation:
In generally let we consider \[r = a \pm b\sin (\theta )\] or \[r
= a \pm b\cos (\theta )\] where \[a > 0\], \[b > 0\] and \[a \ne b\]
Now consider the given equation \[r = 1 + 2\cos \theta \]. Here a=1, and b=2 , graph the limacon as shown
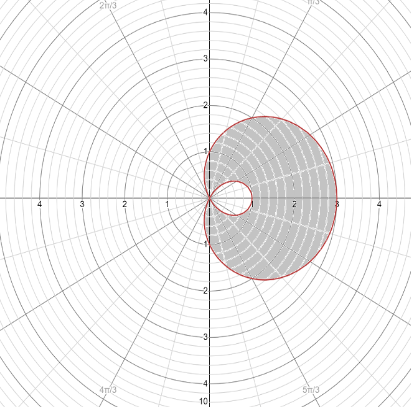
To find the area we use the formula
\[A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r)}^2}d\theta } \]------- (1)
Here the limits points are not given.
Therefore, we have to find the value of
\[\alpha \] and \[\beta \]
Now consider the given equation
\[r = 1 + 2\cos \theta \] ------- (2)
Substitute r=0 in equation (2) we have
\[ \Rightarrow 0 = 1 + 2\cos (\theta )\]
This is written as
\[ \Rightarrow - \dfrac{1}{2} = \cos (\theta )\]
By taking the inverse we have
\[ \Rightarrow {\cos ^{ - 1}}\left( { - \dfrac{1}{2}} \right) = \theta \]
\[ \Rightarrow \theta = \dfrac{{2\pi }}{3}\] and \[\theta = \dfrac{{4\pi }}{3}\].
Therefore \[\theta \] varies from the angle \[\dfrac{{2\pi }}{3}\] to angle \[\dfrac{{4\pi }}{3}\]
\[\therefore \,\,\,\,\left( {\alpha ,\beta } \right) = \left( {\dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3}}
\right)\]----------- (3)
Substituting equation (2) and equation (3) in equation (1) we have
\[A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {{{(1 + 2\cos (\theta ))}^2}d\theta }
\]
Applying the algebraic formula \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\]
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {(1 + 4\cos \left( \theta \right) + 4{{\cos }^2}(\theta ))d\theta } \]
It can be also written as
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {(1 + 4\cos \left( \theta \right) + 2.2{{\cos }^2}(\theta ))d\theta } \]
Apply the double angle formula for the cosine function,\[\cos 2x = 2{\cos ^2}x - 1\,\,\, \Rightarrow
\,\,\,2{\cos ^2}x = \cos 2x + 1\], then
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\left( {1 + 4\cos \left( \theta \right) + 2.\left( {\cos (2\theta ) + 1} \right)} \right)d\theta } \]
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\left( {1 + 4\cos \left(
\theta \right) + 2\cos (2\theta ) + 2} \right)d\theta } \]
On simplifying we have
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\left( {3 + 4\cos \left( \theta \right) + 2\cos (2\theta )} \right)d\theta } \]
Take integral to each term we have
\[ \Rightarrow A = \dfrac{1}{2}\left( {3\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {d\theta } + 4\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\cos \left( \theta \right)d\theta } +
2\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\cos (2\theta )} d\theta } \right)\]
On applying the integration, we have
\[ \Rightarrow A = \dfrac{1}{2}\left( {3\theta + 4\sin \left( \theta \right) + 2\dfrac{{\sin (2\theta)}}{2}} \right)_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}}\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {3\theta + 4\sin \left( \theta \right) + \sin (2\theta )}
\right)_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}}\]
Applying the limit points, we get
\[ \Rightarrow A = \dfrac{1}{2}\left( {3 \cdot \dfrac{{4\pi }}{3} + 4\sin \left( {\dfrac{{4\pi }}{3}}\right) + \sin \left( {2 \cdot \dfrac{{4\pi }}{3}} \right) - 3 \cdot \dfrac{{2\pi }}{3} - 4\sin \left({\dfrac{{2\pi }}{3}} \right) + \sin \left( {2 \cdot \dfrac{{2\pi }}{3}} \right)} \right)\]
On simplifying we get
\[ \Rightarrow A = \dfrac{1}{2}\left( {4\pi + 4\left( { - \dfrac{{\sqrt 3 }}{2}} \right) + \left(
{\dfrac{{\sqrt 3 }}{2}} \right) - 2\pi - 4\left( {\dfrac{{\sqrt 3 }}{2}} \right) - \left( { - \dfrac{{\sqrt 3 }}{2}} \right)} \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {4\pi - \dfrac{{4\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{2} - 2\pi -
\dfrac{{4\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{2}} \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 2 \cdot \dfrac{{4\sqrt 3 }}{2} + 2 \cdot \dfrac{{\sqrt 3 }}{2}} \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 4\sqrt 3 + \sqrt 3 } \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 3\sqrt 3 } \right)\]
\[ \Rightarrow A = \pi - \dfrac{{3\sqrt 3 }}{2}\]
Therefore, the area between the loop of \[r = 1 + 2\cos \theta \] is
\[\therefore \,\,\,A = \pi - \dfrac{{3\sqrt 3 }}{2}\]
Note: The area of a petal for the circle for the polar coordinates is given by \[A =
\dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta } \]. The unit for the area is given as
square unit. In the polar form the coordinates are represented in the form of \[\left( {r,\theta } \right)\]where r represents the radius of the circle and the \[\theta \]represents the angle.
Complete step by step explanation:
In generally let we consider \[r = a \pm b\sin (\theta )\] or \[r
= a \pm b\cos (\theta )\] where \[a > 0\], \[b > 0\] and \[a \ne b\]
Now consider the given equation \[r = 1 + 2\cos \theta \]. Here a=1, and b=2 , graph the limacon as shown
To find the area we use the formula
\[A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r)}^2}d\theta } \]------- (1)
Here the limits points are not given.
Therefore, we have to find the value of
\[\alpha \] and \[\beta \]
Now consider the given equation
\[r = 1 + 2\cos \theta \] ------- (2)
Substitute r=0 in equation (2) we have
\[ \Rightarrow 0 = 1 + 2\cos (\theta )\]
This is written as
\[ \Rightarrow - \dfrac{1}{2} = \cos (\theta )\]
By taking the inverse we have
\[ \Rightarrow {\cos ^{ - 1}}\left( { - \dfrac{1}{2}} \right) = \theta \]
\[ \Rightarrow \theta = \dfrac{{2\pi }}{3}\] and \[\theta = \dfrac{{4\pi }}{3}\].
Therefore \[\theta \] varies from the angle \[\dfrac{{2\pi }}{3}\] to angle \[\dfrac{{4\pi }}{3}\]
\[\therefore \,\,\,\,\left( {\alpha ,\beta } \right) = \left( {\dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3}}
\right)\]----------- (3)
Substituting equation (2) and equation (3) in equation (1) we have
\[A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {{{(1 + 2\cos (\theta ))}^2}d\theta }
\]
Applying the algebraic formula \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\]
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {(1 + 4\cos \left( \theta \right) + 4{{\cos }^2}(\theta ))d\theta } \]
It can be also written as
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {(1 + 4\cos \left( \theta \right) + 2.2{{\cos }^2}(\theta ))d\theta } \]
Apply the double angle formula for the cosine function,\[\cos 2x = 2{\cos ^2}x - 1\,\,\, \Rightarrow
\,\,\,2{\cos ^2}x = \cos 2x + 1\], then
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\left( {1 + 4\cos \left( \theta \right) + 2.\left( {\cos (2\theta ) + 1} \right)} \right)d\theta } \]
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\left( {1 + 4\cos \left(
\theta \right) + 2\cos (2\theta ) + 2} \right)d\theta } \]
On simplifying we have
\[ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\left( {3 + 4\cos \left( \theta \right) + 2\cos (2\theta )} \right)d\theta } \]
Take integral to each term we have
\[ \Rightarrow A = \dfrac{1}{2}\left( {3\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {d\theta } + 4\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\cos \left( \theta \right)d\theta } +
2\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\cos (2\theta )} d\theta } \right)\]
On applying the integration, we have
\[ \Rightarrow A = \dfrac{1}{2}\left( {3\theta + 4\sin \left( \theta \right) + 2\dfrac{{\sin (2\theta)}}{2}} \right)_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}}\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {3\theta + 4\sin \left( \theta \right) + \sin (2\theta )}
\right)_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}}\]
Applying the limit points, we get
\[ \Rightarrow A = \dfrac{1}{2}\left( {3 \cdot \dfrac{{4\pi }}{3} + 4\sin \left( {\dfrac{{4\pi }}{3}}\right) + \sin \left( {2 \cdot \dfrac{{4\pi }}{3}} \right) - 3 \cdot \dfrac{{2\pi }}{3} - 4\sin \left({\dfrac{{2\pi }}{3}} \right) + \sin \left( {2 \cdot \dfrac{{2\pi }}{3}} \right)} \right)\]
On simplifying we get
\[ \Rightarrow A = \dfrac{1}{2}\left( {4\pi + 4\left( { - \dfrac{{\sqrt 3 }}{2}} \right) + \left(
{\dfrac{{\sqrt 3 }}{2}} \right) - 2\pi - 4\left( {\dfrac{{\sqrt 3 }}{2}} \right) - \left( { - \dfrac{{\sqrt 3 }}{2}} \right)} \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {4\pi - \dfrac{{4\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{2} - 2\pi -
\dfrac{{4\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{2}} \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 2 \cdot \dfrac{{4\sqrt 3 }}{2} + 2 \cdot \dfrac{{\sqrt 3 }}{2}} \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 4\sqrt 3 + \sqrt 3 } \right)\]
\[ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 3\sqrt 3 } \right)\]
\[ \Rightarrow A = \pi - \dfrac{{3\sqrt 3 }}{2}\]
Therefore, the area between the loop of \[r = 1 + 2\cos \theta \] is
\[\therefore \,\,\,A = \pi - \dfrac{{3\sqrt 3 }}{2}\]
Note: The area of a petal for the circle for the polar coordinates is given by \[A =
\dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta } \]. The unit for the area is given as
square unit. In the polar form the coordinates are represented in the form of \[\left( {r,\theta } \right)\]where r represents the radius of the circle and the \[\theta \]represents the angle.