Question

Find the angle measure of \[{\text{x}}\]in the following figure

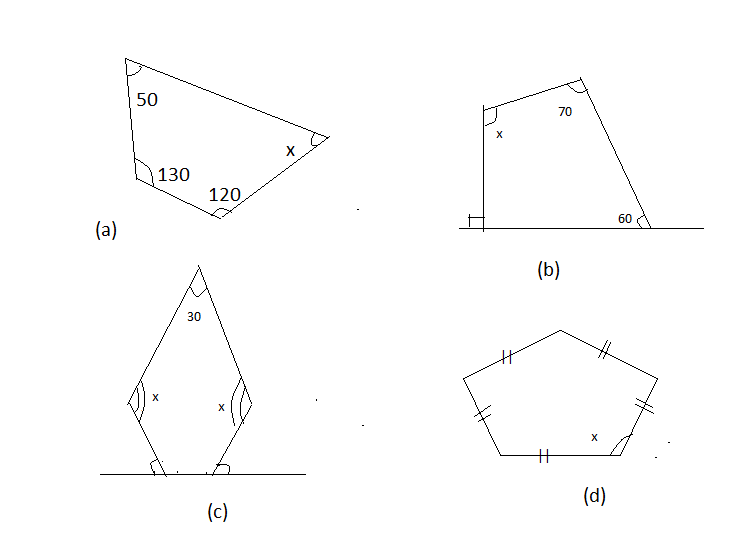
Answer 1

Hint- The sum of interior angles of a polygon is $\left( {{\text{n - 2}}} \right) \times {180^0}$; where n is number of sides in a Polygon.

In this question it is asked the angle of a polygon which is represented by \[{\text{x}}\]in the given figures of polygons
There are two types of polygon in the above question quadrilateral (in fig a, b), pentagon in fig number (c) and regular pentagon in fig number (d)
Sum of Interior angle of Polygon is$\left( {{\text{n - 2}}} \right) \times {180^0}$ (1)
In case of quadrilateral, n is equal to 4 so
 Sum of all internal angle of a quadrilateral will be $\left( {{\text{4 - 2}}} \right) \times {180^0} = {360^0}$ (2)
Solution of Fig (a)
Three angles are known, only \[{\text{x}}\]remains to be found.
$\therefore {50^0} + {130^0} + {120^0} + {\text{x = 30}}{{\text{0}}^0} + {\text{x }}$
This is equal to ${360^0}$
$\therefore {\text{30}}{{\text{0}}^0} + {\text{x = 36}}{{\text{0}}^0}$
$\therefore {\text{x = 6}}{{\text{0}}^0}$ in fig (a)

Solution of Fig (b)
Here two angles are shown ${70^0}{\text{ and }}{60^0}$ and third angle \[{\text{y}}\] is also known which is ${90^0}$ because on a straight line it makes the angle of ${180^0}$. One side angle is ${90^0}$so the other side angle \[{\text{y}}\]will also be ${90^0}$ .
Hence using result (2)
Sum of angles of quadrilateral is
$\therefore {\text{ y}} + {60^0} + {70^0} + {\text{x }}$
$\therefore {90^0} + {60^0} + {70^0} + {\text{x = 22}}{{\text{0}}^0} + {\text{x }}$
This is equal to ${360^0}$
$\therefore {\text{22}}{{\text{0}}^0} + {\text{x = 36}}{{\text{0}}^0}$
$\therefore {\text{x = 36}}{{\text{0}}^0} - {\text{22}}{{\text{0}}^0}$
$\therefore {\text{x = 14}}{{\text{0}}^0}$ In fig (b)

Solution of Fig (c)
As given in the question, one angle of pentagon is ${30^ \circ }$, others two equal angles will be \[{\text{x}}\]and remaining others angles Y can be find easily because on straight line it makes the angle of ${180^0}$
$\therefore {30^0} + {\text{y = 18}}{{\text{0}}^0}$
$\therefore {\text{y = 15}}{{\text{0}}^0}$
In case of pentagon, n is equal to 5, so using result (1)
Sum of Interior angle of Pentagon is$\left( {{\text{5 - 2}}} \right) \times {180^0} = {540^0}$ (3)
So using this result
$\therefore {\text{x + x}} + {\text{y}} + {\text{y}} + {30^0}{\text{ = 54}}{0^0}{\text{ }}$
$\therefore {\text{x + x}} + {150^0} + {150^0} + {30^0}{\text{ = 54}}{0^0}{\text{ }}$
$\therefore 2{\text{x + 33}}{0^0}{\text{ = 54}}{0^0}{\text{ }}$
$\therefore 2{\text{x + 33}}{0^0}{\text{ = 54}}{0^0}{\text{ }}$
$\therefore 2{\text{x = 21}}{{\text{0}}^0}{\text{ }}$
$\therefore {\text{x = 10}}{{\text{5}}^0}{\text{ }}$in fig (c)
Solution of Fig (d)
This is a regular pentagon because all its sides and angles are equal. Hence its each angle will be equal.
$\therefore {\text{x + x}} + {\text{x + x + x = 54}}{0^0}{\text{ }}$
$\therefore 5{\text{x = 54}}{0^0}{\text{ }}$
$\therefore {\text{x = 10}}{{\text{8}}^0}{\text{ }}$
Alternative- In case of regular polygon, expression ${\frac{{\left( {{\text{n - 2}}} \right) \times 180}}{{\text{n}}}^0}$ can also be used to find each angle.
Note: -
Whenever we face such types of problems the key concept we have to remember is that, always remember the formula of sum of internal angles of a polygon which is stated above, then using this formula calculate the unknown angle of a polygon.