Question

Find the \[{\text{A}}{\text{.}}\] Probability of the pointer stopping on \[D\] in spinning a wheel if it has $A,A,D,B,C$written on it?
\[{\text{B}}{\text{.}}\] Probability of getting an ace from a well shuffled deck of $52$ playing
cards?
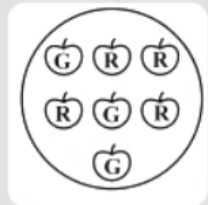
\[{\text{C}}{\text{.}}\] Probability of getting a red apple from the figure given.

Answer 1

Hint: - Probability is equal to the ratio of number of outcomes to total possible outcomes.
According to the question, we have given that ${\text{A}}{\text{.}}$ The pointer can stop at one of the following regions$A,A,D,B,C$ .
But if we can recall we will find that only in the $1$ case, the pointer will stop at D.
So, probability for this case will be
$P = \dfrac{1}{5}$
\[{\text{B}}{\text{.}}\] We all know that there are $52$ cards:
We have $4$ ace cards over $52$ cards,
So, probability of getting an ace card
$ \Rightarrow \dfrac{4}{{52}} = \dfrac{1}{{13}}$
\[{\text{C}}{\text{.}}\]There are a total of $7$ apples, out of which $4$ are red and $3$ are green.
Probability of red apple $ \Rightarrow \dfrac{4}{7}$

Note – Probability can never be greater than 1 nor it can be less than 0. In this type of question only
 smart thinking is required. A deck of cards has $52$mainly $4$ sets each of $13$ cards i.e
spades,clubs,diamonds and hearts. Probability is equal to the ratio of number of outcomes to total
 number of outcomes.