Question

Find acceleration in the given cases.

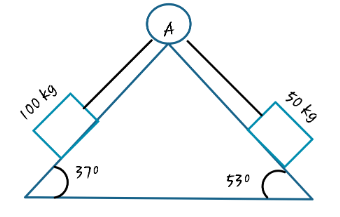
Answer 1

Hint: First write the equation of motion of each block. Take into consideration the tension produced in the string, weight (mg) component along the inclined plane.
TENSION: whenever any string is tight then the end of the string pulls whatever is connected to them in inward direction. This inward pulling force of the string on the object is called a tension force. It depends on mass, as mass increases tension also increases.
Remember that the heavy block will move down and the light block will slide up. According to this, it gives direction to the acceleration produced.

Complete step by step answer

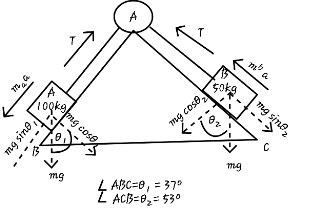
Let T, be the tension produced in the string and ‘a’ be the acceleration produced in each block.
Therefore, equation of motion of block A can be written as
 $ \begin{align}
  & {{m}_{A}}g\sin \theta -T={{m}_{A}}a \\
 & {{m}_{A}}g\sin 37{}^\circ -T={{m}_{A}}a\text{ }............\text{(1)} \\
 & \text{Equation of motion for block B is:-} \\
 & T-{{m}_{B}}g\sin {{\theta }_{2}}={{m}_{B}}a\text{ } \\
 & T-{{m}_{B}}g\sin 53{}^\circ ={{m}_{B}}a\text{ }.............\text{(2)} \\
\end{align} $
Adding equations 1. and 2. Gives,
 $ \begin{align}
  & g({{m}_{A}}\sin 37{}^\circ -{{m}_{b}}\sin 53{}^\circ )=({{m}_{A}}+{{m}_{B}})a \\
 & g(100\times \dfrac{3}{5}-50\times \dfrac{4}{5})=(100+50)a \\
 & 10(60-40)=150a \\
 & a=\dfrac{200}{15}=\dfrac{4}{3}m/{{s}^{2}} \\
 & \text{Thus acceleration of block= 4/3 ms}_{^{{}}}^{-2} \\
\end{align} $ .

Additional Information
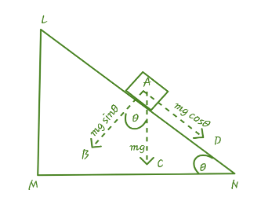
Consider the situation as given in the following diagram.

 $ \begin{align}
  & Here,\angle LMN=\angle BAC=\theta \\
 & \\
\end{align} $
Because, the angle between the two lines is equal to the angle between the normal of that line.
 $ \text{As here, MN}\bot \text{AC and BA}\bot \text{AD} $
Thus component along AN = mg $ \text{sin }\!\!\theta\!\!\text{ } $
Component along AB = mg $ \text{cos }\!\!\theta\!\!\text{ } $ .

Note
Equations 1 and 2 are taken according to the direction of acceleration produced in each block. Thus taking into account which force is dominant, according to which large value of force is to be subtracted from the small value, to get the resultant force.
Remember that the second law of Newton states that the acceleration of an object is dependent upon two variables - the net force acting upon the object and the mass of the object.