Question

Fill in the blanks using the correct word given in the brackets: All __________ triangles are similar. (Isosceles, Equilateral)

Answer 1

Hint: The question is related to the similarity of triangles. Try to recall the AAA criterion for similarity of triangles and use the property that all the internal angles of an equilateral triangle measure ${{60}^{o}}$.

Complete step-by-step answer:
Before proceeding with the solution, we must understand the concept of similarity of triangles. Two triangles are said to be similar if their angles are equal and their corresponding sides are proportional. Consider the two triangles given in the figure:

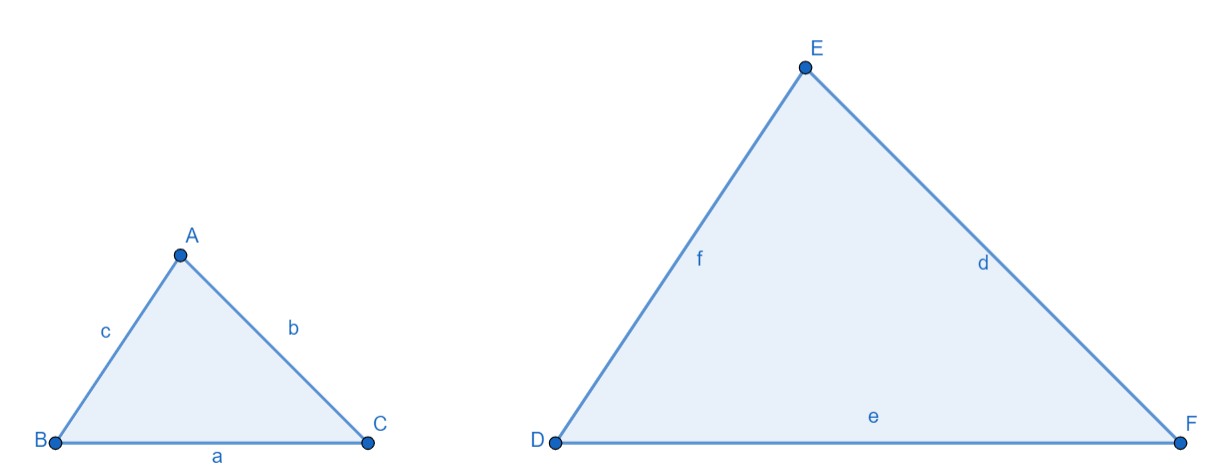
The two triangles $\Delta ABC$ and $\Delta EDF$ are similar if $\dfrac{a}{e}=\dfrac{b}{d}=\dfrac{c}{f}$ . Also, if the two triangles are similar then, $\measuredangle A=\measuredangle E;\measuredangle B=\measuredangle D$ and $\measuredangle C=\measuredangle F$.
Now, we know that in an isosceles triangle, the base angles are equal. But it is not compulsory that the angles will be equal between two triangles.
In case of an equilateral triangle, the three angles of the triangle are equal and their measure is fixed, i.e. ${{60}^{o}}$ . So, in all equilateral triangles, the measure of the angles is fixed and hence, the angles of two equilateral triangles will be equal. So, two equilateral triangles will always be similar.
Hence, all equilateral triangles are similar.

Note: Congruence and similarity of triangles are not the same. A congruent triangle is necessarily similar, but a similar triangle may or may not be congruent. For congruence of triangles, the corresponding sides of the two triangles should be equal, whereas for similarity the corresponding sides of the two triangles should be proportional. Students generally get confused between the two concepts. Such confusion should be avoided.