Question

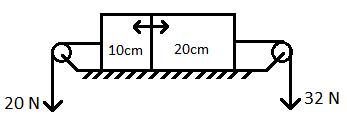
Figure shows a uniform rod of length 30cm having a mass of 3.0kg. The strings shown in the figure are pulled by constant forces of 20N and 32N. Find the force exerted by the 20cm part of the rod on the 10cm part. All the surfaces are smooth and the strings and the pulleys are light  

Answer 1

Hint: We are given the length and mass of a rod which is connected to pulleys at both ends. The force exerted by both the pulleys is also given to us. The rod is made into two parts with different lengths and we are asked to find the force exerted by one part on the other part. We know that according to Newton’s third law the force exerted by two parts on each other will be the same. By drawing the free body diagram and equating the forces we will get the required solution.

Formula used:
$F=ma$

Complete step-by-step answer:
In the question we are given a rod of length 30 cm and mass 3.0 kg.
The rod is split into two parts, one with 10 cm length and the other with 20 cm length.
Let ‘\[{{m}_{1}}\]’ be the mass of 10 cm part and ‘\[{{m}_{2}}\]’ be the mass of 20 cm part.
Then we have ‘\[{{m}_{1}}\]’ as,
\[{{m}_{1}}=\dfrac{10}{30}\times 3\]
$\Rightarrow {{m}_{1}}=1kg$
And we have ‘\[{{m}_{2}}\]’ as,
\[{{m}_{2}}=\dfrac{20}{30}\times 3\]
$\Rightarrow {{m}_{2}}=2kg$
Now let us draw the free body diagram of the two parts.

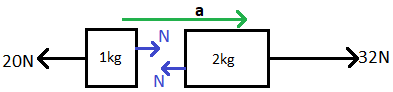
There is a 20N force acting towards left on the 10 cm part and a 32 N force acting towards right in the 20 cm part.
We know that the contact force applied by the 20 cm part on the 10 cm part will be equal and opposite to the contact force applied by the 10 cm part on the 20 cm part.
This contact force is given as ‘N’ in the figure.
The acceleration of the body will be towards the right direction because the magnitude of force is higher in that direction.
From the free body diagram the forces acting on the 10 cm part is,
$F=N-20$ and $F={{m}_{1}}a$
By equating these two forces we get,
$\Rightarrow N-20={{m}_{1}}a$
$\Rightarrow N-20=a$
This is the free body diagram equation of 10 cm part.
The forces acting on the 20 cm part from the free body diagram is,
$F=32-N$ and $F={{m}_{2}}a$
Therefore the total force on 20 cm part will be,
$\Rightarrow 32-N={{m}_{2}}a$
$\Rightarrow 32-N=2a$
This is the free body diagram equation of 20 cm part.
By adding the two free body diagram equations, we get
$N-20+32-N=3a$
$\Rightarrow 12=3a$
From this equation we get the acceleration as,
$\Rightarrow a=\dfrac{12}{3}=4m/{{s}^{2}}$
In the question we are asked to find the force exerted by the 20cm part of the rod on the 10cm part. This is the contact force applied by 20 cm part on the 10 cm part which is given by the equation,
$N-20=a$
By applying the value for acceleration we get,
$\Rightarrow N=4+20=24N$
Therefore the force exerted by the 20cm part of the rod on the 10cm part is 24 N.

Note: To solve this question we construct the free body diagram of two parts of the rod. A free body diagram is a diagram which we use to represent the magnitude and direction of all the forces acting on a body. Thus by drawing the free body diagram it will be easy for us to equate the forces.
In this question we say that the contact force applied by the 20 cm part on the 10 cm part is equal and opposite to the contact force applied by the 10 cm part on the 20 cm part. We say this according to Newton’s third law of motion. The law states that for each action in nature there will always be an equal and opposite reaction.