Question

Figure represents a square carrying charges $ + q$ , $ + q$ , $ - q$ , $ - q$ at its four corners as shown. Then the potential will be zero at points.

A. A, B, C, P and Q
B. A, B and C
C. A, P, C and Q
D. P, B and Q

Answer 1

Hint: Calculate the potential at each point; P, Q, A, B and C. Then check where the potential is zero and accordingly choose the correct option. The potential due to point charge $q$ at a distance $r$ is given as $V = \dfrac{{Kq}}{r}$ where $K$ is a constant.

Formula used:
$V = \dfrac{{Kq}}{r}$
Where $V$ is the potential
$K$ is a constant.
$q$ point charge
$r$ is distance of point from the charge

Complete step by step answer:
A point charge has a field up to infinite distance. Any charged body in that field will experience some force. The electric potential at a point is the electric potential energy at that point due to a point charge divided by the charge.
Mathematically it is written as:
 $V = \dfrac{{Kq}}{r}$
Let us calculate the electric potential at each of the six points and check which of them is zero.
In order to calculate the electric potential, we will have to calculate the distance of each point from all the point charges:
As the given figure is a square therefore, we have symmetry between different points.
Let the length of the side of square be s;

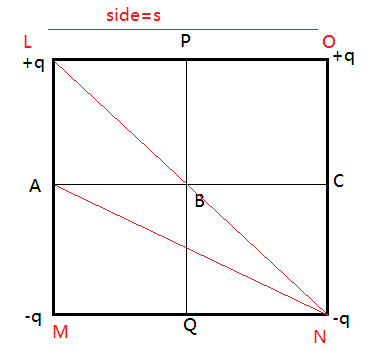
Let the square be LMNO, now due symmetry we have the distances;
$LM = MN = NO = OL = s$
$LN = MO = \sqrt 2 s$
For distance of AN, we have right angled triangle AMN with:
$AM = \dfrac{s}{2}$ ; $MN = s$
Using Pythagoras theorem, we have
$AN = \sqrt {{{\left( s \right)}^2} + {{\left( {\dfrac{s}{2}} \right)}^2}} $
$ \Rightarrow AN = \sqrt {\dfrac{5}{2}} s$
By symmetry we have:
$AN = MC = LC = OA = LQ = OQ = \sqrt {\dfrac{5}{2}} s$
For point B, we have distances as follows:
$LB = MB = NB = OB = \dfrac{s}{{\sqrt 2 }}$
Let us now find the potential at point A ${V_A}$ ;
${V_A} = {V_{due\,\,to\,N}} + {V_{due\,to\,O}} + {V_{due\,to\,L}} + {V_{due\,to\,M}}$
$\implies {V_A} = - \dfrac{{Kq}}{{\dfrac{{\sqrt 5 }}{2}s}} + \dfrac{{Kq}}{{\dfrac{{\sqrt 5 }}{2}s}} + \dfrac{{Kq}}{{\dfrac{s}{2}}} - \dfrac{{Kq}}{{\dfrac{s}{2}}}$
${V_A} = 0$
The potential at point A is zero.
Point C is symmetrical to point A, therefore
${V_C} = 0$
Potential at point B;
${V_B} = {V_{due\,\,to\,\,L}} + {V_{due\,to\,M}} + {V_{due\,to\,N}} + {V_{due\,to\,O}}$
$\implies {V_B} = \dfrac{{Kq}}{{\dfrac{s}{{\sqrt 2 }}}} - \dfrac{{Kq}}{{\dfrac{s}{{\sqrt 2 }}}} - \dfrac{{Kq}}{{\dfrac{s}{{\sqrt 2 }}}} + \dfrac{{Kq}}{{\dfrac{s}{{\sqrt 2 }}}}$
${V_B} = 0$
The potential at point B is also zero.
Potential at point P will be equal to potential at point Q;
Distance of point Q from different charges are as follows:
$MQ = QN = \dfrac{s}{2}$
$LQ = OQ = \sqrt {\dfrac{5}{2}} s$
$\implies {V_Q} = {V_{due\,\,to\,\,L}} + {V_{due\,to\,M}} + {V_{due\,to\,N}} + {V_{due\,to\,O}}$
$\implies {V_Q} = \dfrac{{Kq}}{{\dfrac{{\sqrt 5 }}{2}s}} - \dfrac{{Kq}}{{\dfrac{s}{2}}} - \dfrac{{Kq}}{{\dfrac{s}{2}}} + \dfrac{{Kq}}{{\dfrac{{\sqrt 5 }}{2}s}}$
Clearly, ${V_Q} \ne 0$
Similarly, ${V_P} \ne 0$
Therefore, the potential is zero at points A, B and C

So, the correct answer is “Option B”.

Note:
It can also be easily observed that when opposite charges are at equal distance, then the potential at that point due opposite charges will be zero. Be careful while calculating the distance between the charge and the point of observation. A body lying at midpoint of line joining two equal charges experiences zero force.