Question

Explain the formation of stationary waves by analytical method. Show the formation of the stationary wave diagrammatically.

Answer 1

Hint: In the analytical method of studying the formation of stationary waves, we consider two progressive waves incident on each other from opposite directions. The resultant of this superposition is calculated by using the superposition principle.

Complete step-by-step solution
Consider two waves having the same amplitude and frequency traveling towards each other as shown in the diagram.

When they reach each other, they undergo interference where they superimpose on each other. The resultant of this type of superimposition is the stationary waves. As the name implies, they are not traveling but stay stationary.
Consider a traveling wave of the following form.
\[{y_1} = A\sin 2\pi \left( {\dfrac{t}{T} - \dfrac{x}{\lambda }} \right)\]
Here A is the amplitude of this wave while $\lambda $ represents the wavelength of this wave. It is traveling in the positive x-direction.
Now consider this same wave getting reflected from an obstruction as a result of which it starts travelling back in the negative x direction. It can be written as
\[{y_2} = A\sin 2\pi \left( {\dfrac{t}{T} + \dfrac{x}{\lambda }} \right)\]
Now these two waves will superimpose on each other and their resultant is given by the principle of superposition in the following way.
$y = {y_1} + {y_2}$
Now inserting the known expressions and solving for the resultant displacement, we get
$y = A\sin 2\pi \left( {\dfrac{t}{T} - \dfrac{x}{\lambda }} \right) + A\sin 2\pi \left( {\dfrac{t}{T} + \dfrac{x}{\lambda }} \right)$
Using the identity, $\sin A + \sin B = 2\sin \left\{ {\dfrac{{A + B}}{2}} \right\}\cos \left\{ {\dfrac{{A + B}}{2}} \right\}$, we get
$\begin{gathered}
  y = A\left[ {2\sin \left( {\dfrac{{2\pi t}}{T}} \right)\cos \left( {\dfrac{{2\pi x}}{\lambda }} \right)} \right] \\
  y = A'\sin \left( {\dfrac{{2\pi t}}{T}} \right){\text{ }}...{\text{(i)}} \\
\end{gathered} $
Here $A' = 2A\cos \left( {\dfrac{{2\pi x}}{\lambda }} \right)$
The equation (i) is known as the equation of stationary waves having amplitude A’. From this equation, we understand that we will get some points of maximum and minimum displacement in the stationary wave called antinodes and nodes respectively.

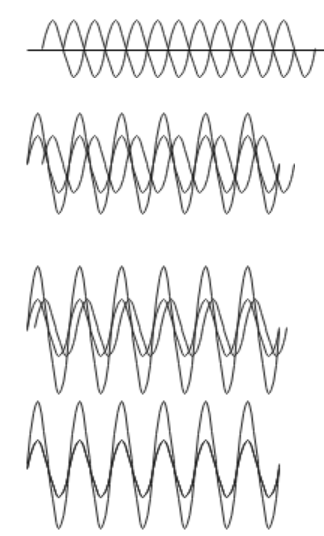
These diagrams show the resultant stationary waves formed when the incident and reflected wave superimpose at different phase angles.

Note: The waves are stationary because they are formed by two waves having equal motion but in opposite directions. The equal and opposite nature of two waves results in the stationary nature of the stationary waves. This phenomenon is observed when the incident and reflected waves superimpose on each other.