
Every gram of wheat provides 0.1g of proteins and 0.25g of carbohydrates. The corresponding values of rice are 0.05g and 0.5g respectively. Wheat cost Rs.4 per kg and rice Rs.6. The minimum daily requirements of proteins and carbohydrates for an average child are 50g and 200g respectively. Then in what quantities should wheat and rice be mixed in the daily diet to provide a minimum daily requirement of proteins and carbohydrates at minimum cost.
Answer
552.3k+ views
Hint: We solve this by linear programming that is by drawing a graph of inequalities. Let ‘\[x\]’ grams of wheat are mixed and ‘\[y\]’ grams of rice are mixed. Using this we will get two inequities. We find the values by equating ‘\[x\]’ to zero, we get ‘\[y\]’ and vice versa. Plotting a graph we can find the minimum cost.
Complete step-by-step solution:
Let \[x\] gram of wheat and y grams of rice are mixed in a daily diet.
Given, every gram of wheat provides 0.1g of proteins and every gram of rice gives 0.05g of proteins. Therefore, \[x\] grams of wheat and \[y\] grams of rice will provide \[0.1x + 0.05y\] grams of proteins. But the minimum requirement of proteins is 50g.
That is, \[0.1x + 0.05y \geqslant 50\].
To get the simplified form multiply and divide by 100 on each term,
\[ \Rightarrow 0.1x \times \dfrac{{100}}{{100}} + 0.05y \times \dfrac{{100}}{{100}} \geqslant 50 \times \dfrac{{100}}{{100}}\]
\[ \Rightarrow \dfrac{{10x}}{{100}} + \dfrac{{5y}}{{100}} \geqslant 50\]
Cancelling, we get,
\[ \Rightarrow \dfrac{x}{{10}} + \dfrac{y}{{20}} \geqslant 50\] ----- (1)
Similarly \[x\]grams of wheat and \[y\]grams of rice will provide\[0.25x + 0.5y\]grams of carbohydrates and the minimum daily requirement is 200 grams.
That is, \[0.25x + 0.5y \geqslant 200\].
To get the simplified form multiply and divide by 100 on each term,
\[ \Rightarrow 0.25x \times \dfrac{{100}}{{100}} + 0.5y \times \dfrac{{100}}{{100}} \geqslant 200 \times \dfrac{{100}}{{100}}\]
\[ \Rightarrow \dfrac{{25x}}{{100}} + \dfrac{{50y}}{{100}} \geqslant 200\]
Cancelling, we get:
\[ \Rightarrow \dfrac{x}{4} + \dfrac{y}{2} \geqslant 200\] ----- (2)
Also quantities of wheat and rice will never be negative.
\[x \geqslant 0\]and \[y \geqslant 0\]
It is given that wheat costs Rs.4 per kg and rice Rs.6 per kg. So we have,
\[\dfrac{{4x}}{{1000}} + \dfrac{{6y}}{{1000}} = z\]minimum.
Subject to the constraints
\[\dfrac{x}{{10}} + \dfrac{y}{{20}} \geqslant 50\], \[\dfrac{x}{4} + \dfrac{y}{2} \geqslant 200\], \[x \geqslant 0\], \[y \geqslant 0\].
Now to find the points ,
Put \[x = 0\] in equation (1) we have,
\[ \Rightarrow \dfrac{0}{{10}} + \dfrac{y}{{20}} = 50\]
\[ \Rightarrow \dfrac{y}{{20}} = 50\]
\[ \Rightarrow y = 1000\]. Thus we have (0, 1000).
Similarly put \[y = 0\] in equation (1)
\[ \Rightarrow \dfrac{x}{{10}} = 50\]
\[ \Rightarrow x = 500\]. Thus we have (500, 0).
Similarly put \[x = 0\] in equation (2), we have:
\[ \Rightarrow \dfrac{y}{2} = 200\]
\[ \Rightarrow y = 400\]. Thus we have (0, 400)
Similarly put \[y = 0\] in equation (2)
\[ \Rightarrow \dfrac{x}{4} = 200\]
\[ \Rightarrow x = 800\]. Thus we have (800, 0).
Thus we have the points, \[(0,1000)\], \[(500,0)\], \[(0,400)\]and \[(800,0)\]. Plotting a graph for this.
Scale: X-axis = 1 unit =100 units, Y-axis = 1 unit =100 units.
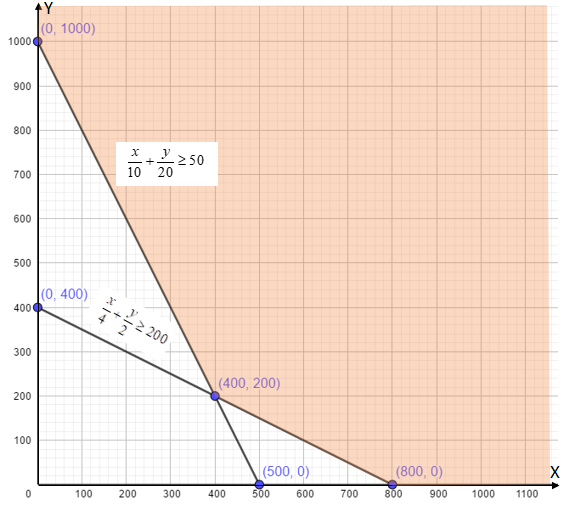
The values of the objective function at these points are given in the following table:
Clearly, Z is minimum for \[x = 400\]grams of wheat and \[y = 200\] grams of rice. The minimum cost is Rs.\[2.8\]
Note: All we did in above is converting the given word problem into inequality problems. As we know that we need a point to join a line, hence we find the inequality value at ‘x’ is zero and then at ‘y’ is zero. Also if they mention minimum we take greater than or equal to(\[ \geqslant \]). If they mention maximum we take less than or equal to (\[ \leqslant \]).
Complete step-by-step solution:
Let \[x\] gram of wheat and y grams of rice are mixed in a daily diet.
Given, every gram of wheat provides 0.1g of proteins and every gram of rice gives 0.05g of proteins. Therefore, \[x\] grams of wheat and \[y\] grams of rice will provide \[0.1x + 0.05y\] grams of proteins. But the minimum requirement of proteins is 50g.
That is, \[0.1x + 0.05y \geqslant 50\].
To get the simplified form multiply and divide by 100 on each term,
\[ \Rightarrow 0.1x \times \dfrac{{100}}{{100}} + 0.05y \times \dfrac{{100}}{{100}} \geqslant 50 \times \dfrac{{100}}{{100}}\]
\[ \Rightarrow \dfrac{{10x}}{{100}} + \dfrac{{5y}}{{100}} \geqslant 50\]
Cancelling, we get,
\[ \Rightarrow \dfrac{x}{{10}} + \dfrac{y}{{20}} \geqslant 50\] ----- (1)
Similarly \[x\]grams of wheat and \[y\]grams of rice will provide\[0.25x + 0.5y\]grams of carbohydrates and the minimum daily requirement is 200 grams.
That is, \[0.25x + 0.5y \geqslant 200\].
To get the simplified form multiply and divide by 100 on each term,
\[ \Rightarrow 0.25x \times \dfrac{{100}}{{100}} + 0.5y \times \dfrac{{100}}{{100}} \geqslant 200 \times \dfrac{{100}}{{100}}\]
\[ \Rightarrow \dfrac{{25x}}{{100}} + \dfrac{{50y}}{{100}} \geqslant 200\]
Cancelling, we get:
\[ \Rightarrow \dfrac{x}{4} + \dfrac{y}{2} \geqslant 200\] ----- (2)
Also quantities of wheat and rice will never be negative.
\[x \geqslant 0\]and \[y \geqslant 0\]
It is given that wheat costs Rs.4 per kg and rice Rs.6 per kg. So we have,
\[\dfrac{{4x}}{{1000}} + \dfrac{{6y}}{{1000}} = z\]minimum.
Subject to the constraints
\[\dfrac{x}{{10}} + \dfrac{y}{{20}} \geqslant 50\], \[\dfrac{x}{4} + \dfrac{y}{2} \geqslant 200\], \[x \geqslant 0\], \[y \geqslant 0\].
Now to find the points ,
Put \[x = 0\] in equation (1) we have,
\[ \Rightarrow \dfrac{0}{{10}} + \dfrac{y}{{20}} = 50\]
\[ \Rightarrow \dfrac{y}{{20}} = 50\]
\[ \Rightarrow y = 1000\]. Thus we have (0, 1000).
Similarly put \[y = 0\] in equation (1)
\[ \Rightarrow \dfrac{x}{{10}} = 50\]
\[ \Rightarrow x = 500\]. Thus we have (500, 0).
Similarly put \[x = 0\] in equation (2), we have:
\[ \Rightarrow \dfrac{y}{2} = 200\]
\[ \Rightarrow y = 400\]. Thus we have (0, 400)
Similarly put \[y = 0\] in equation (2)
\[ \Rightarrow \dfrac{x}{4} = 200\]
\[ \Rightarrow x = 800\]. Thus we have (800, 0).
Thus we have the points, \[(0,1000)\], \[(500,0)\], \[(0,400)\]and \[(800,0)\]. Plotting a graph for this.
Scale: X-axis = 1 unit =100 units, Y-axis = 1 unit =100 units.

The values of the objective function at these points are given in the following table:
| Corner points | Value of \[z = \dfrac{{4x}}{{1000}} + \dfrac{{6y}}{{1000}}\] |
| \[(800,0)\] | \[z = \dfrac{{4 \times 800}}{{1000}} + \dfrac{{6 \times 0}}{{1000}} = \dfrac{{32}}{{10}} = 3.2\] |
| \[(400,200)\] | \[z = \dfrac{{4 \times 400}}{{1000}} + \dfrac{{6 \times 200}}{{1000}} = 1.6 + 1.2 = 2.8\] |
| \[(0,1000)\] | \[z = \dfrac{{4 \times 0}}{{1000}} + \dfrac{{6 \times 1000}}{{1000}} = 6\] |
Clearly, Z is minimum for \[x = 400\]grams of wheat and \[y = 200\] grams of rice. The minimum cost is Rs.\[2.8\]
Note: All we did in above is converting the given word problem into inequality problems. As we know that we need a point to join a line, hence we find the inequality value at ‘x’ is zero and then at ‘y’ is zero. Also if they mention minimum we take greater than or equal to(\[ \geqslant \]). If they mention maximum we take less than or equal to (\[ \leqslant \]).
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




