Question

What is equivalent resistance? Derive the expression for effective resistance of two resistors connected in parallel.

Answer 1

Hint:The word “equivalent” means the total. To derive the expression for effective resistance in the parallel combination of the two resistors, draw the circuit diagram of the two resistors connected parallel to each other. Use Kirchhoff’s current law to express the current at the junction to derive the expression.

Complete step by step answer:
Equivalent resistance is nothing but the total resistance in the circuit. If we connect the number of resistors one after another to the same wire, the total resistance of the wire increases because the resistance of each resistor adds up. Also, when we connect the number of resistors parallel to each other, the total resistance of the circuit decreases. Thus, we can say that the equivalent resistance is the resistance encountered by the whole circuit.Let the two resistors are connected in parallel combination as shown in the figure below.

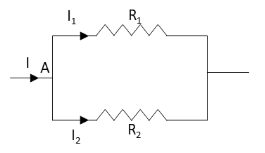
We know that the voltage in the parallel arm remains the same. Therefore, the voltage across the resistor \[{R_1}\] and the voltage across the resistor \[{R_2}\] is the same.Applying Kirchhoff’s current law at the junction A in the above circuit, we get,
\[I = {I_1} + {I_2}\]
Using Ohm’s law, we can write the above equation as,
\[\dfrac{V}{{{R_{eff}}}} = \dfrac{V}{{{R_1}}} + \dfrac{V}{{{R_2}}}\]
Here, \[{R_{eff}}\] is the effective resistance of the two resistors and V is the voltage which is the same across the two resistors.
Simplifying the above equation, we get,
\[\dfrac{1}{{{R_{eff}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\]
\[ \therefore {R_{eff}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\]
This is the required expression for the effective resistance of the two resistors connected parallel to each other.

Note:Students can also derive the expression for effective resistance in the series combination of the two resistors in the same manner as we have done in the above section. Remember, the current remains the same in series combination and the voltage remains the same in parallel combination. This is the key to derive the expression for both effective resistances in the series combination and the parallel combination. Also, students should remember KVL and KCL.