Question

Draw the graph of the equation $y - 2x = 4$ and then answer the following,
A. Does the point (2,8) lie on the line? Is (2,8) a solution of the equation? Check by substituting (2,8) in the equation.
B. Does the point (4,2) lie on the line? Is (4,2) a solution of the equation? Check algebraically also.

Answer 1

Hint: we have to draw the equation of line $y - 2x = 4$ for that we have to find the points A, B, and C by substituting $x = 0,1, - 2$ in the given equation of line, then we have to plot the points A, B, and C on the graph paper and joint them to get the straight line BC as show in graph sheet. This line is the required graph of the equation $y - 2x = 4$
Then we plot the point (2,8) on the graph paper and check it by algebraically by putting that points in the given equation $y - 2x = 4$
Similar, we plot the point (4,2) on the graph paper and check it by algebraically by putting that points in the given equation $y - 2x = 4$

Complete answer:
Step 1: first of all we have to find the points A, B, and C by substituting $x = 0,1, - 2$ in the given equation $y - 2x = 4$
So, by substituting $x = 0$ we get,
$
   \Rightarrow y - 2(0) = 4 \\
   \Rightarrow y = 4 \\
 $
So, we get the point A = $(0,4)$
Step 2: Now, we have to put $x = 1$ and find the value of point C as according to the solution step 1. Hence,
$
   \Rightarrow y - 2(1) = 4 \\
   \Rightarrow y = 4 + 2 \\
   \Rightarrow y = 6 \\
 $
Hence, point C is $(1,6)$
Step 3: Now, we have to put $x = - 2$ and find the value of point B as according to the solution step 1. Hence,
$
   \Rightarrow y - 2( - 2) = 4 \\
   \Rightarrow y = 4 - 4 \\
   \Rightarrow y = 0 \\
 $
Hence, point B is $( - 2,0)$
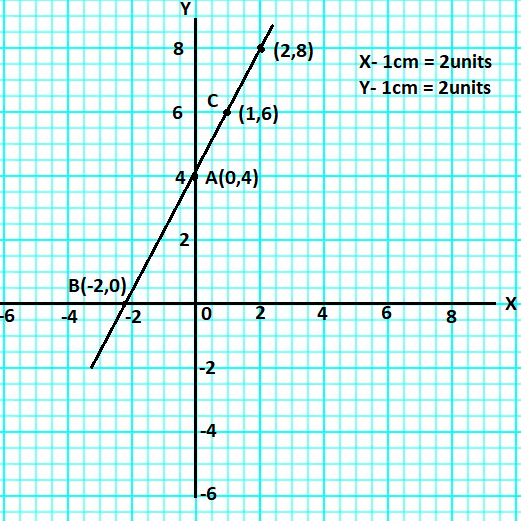
Step 4: Now, we have to draw the graph for all the three points as obtained as A, B, and C in the previous solution steps which is as below:
Step 5: Now, we have to substitute the points $(2,8)$ in the expression $y - 2x = 4$ so, check that the points satisfy the expression or not. Hence,
$
   \Rightarrow 8 - 2(2) = 4 \\
   \Rightarrow 4 = 4 \\
 $
Hence, $(2,8)$ is the solution for the given expression $y - 2x = 4$ which satisfies the expression.

Step 6: Now, we have to substitute the points $(4,2)$ in the expression $y - 2x = 4$ so, check that the points satisfy the expression or not. Hence,
$
   \Rightarrow 4 - 2(2) = 4 \\
   \Rightarrow 0 \ne 4 \\
 $
Hence, $(4,2)$ is not the solution for the given expression $y - 2x = 4$ which does not satisfy the expression.

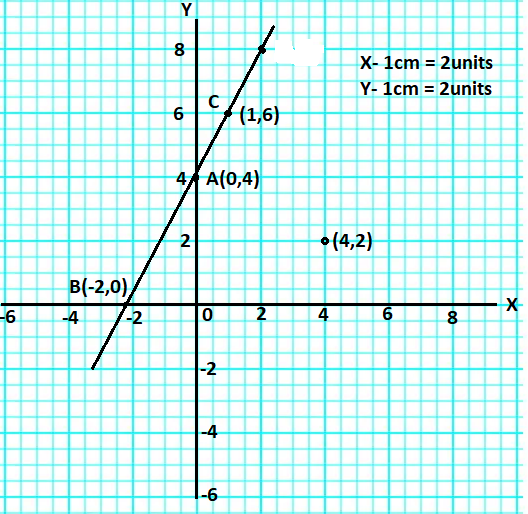
Final solution: Hence, we have to be satisfied by the graph and by the algebraically that point $(2,8)$ lies on the given equation of line and point $(4,2)$ does not lie on the line.

Note:
We have to find the points A, B and C to plot the graph of the given equation of line $y - 2x = 4$ we can be determined by substituting $x = 0,1, - 2$ in the given equation of line.
To satisfy that the points $(2,8)$ and $(4,2)$ lies on the given equation of line $y - 2x = 4$ by substituting $x = 2,y = 8$ and $x = 4,y = 2$ in the given equation of line $y - 2x = 4$.