Question

Draw any polygon and shade its interior.

Answer 1

Hint: Start with the correct definition of a polygon. Then choose the number of sides and draw accordingly.

Let us start by defining what a polygon actually is.
So, a figure is a polygon, if it is a simple closed figure made up entirely of finite number of line segments.
A polygon should have at least three sides and vertices and at max any number of finite sides and vertices.
For e.g.: A polygon with three sides is called a Triangle.
A polygon with four sides is called a Rectangle.
A polygon with five sides is called a Pentagon.
A polygon with six sides is called a Hexagon and so on.
For this question, let us draw a polygon with five sides called a Pentagon.
So, let us start by making a line segment and name it AB.

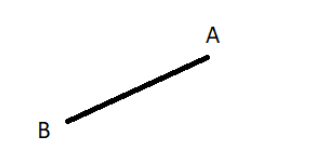
Now, draw another line segment starting from B and name the other end C.

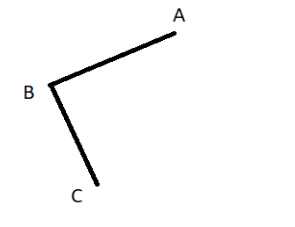
Similarly, draw another line segment starting from C and name the other end D.

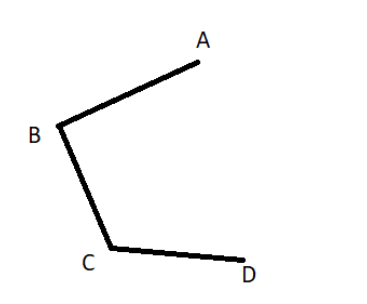
Again, draw a line segment starting from D and name the other end E.

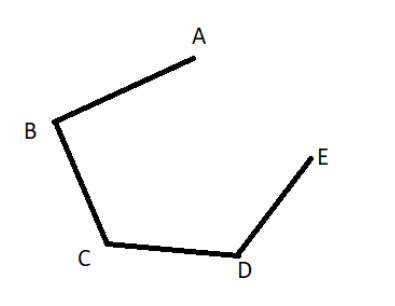
Now, since we have 5 vertices from A to E already, but we only have 4 sides. So, we do not create another vertex and just join points A and E.

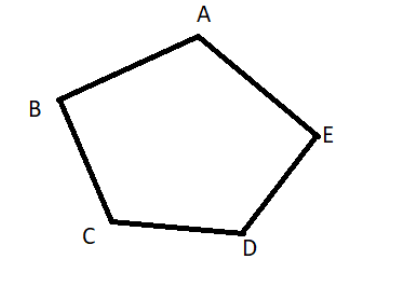
This is our Pentagon.
Now let us shade its interior.

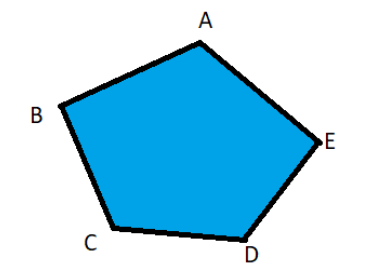
So ABCDE is our required pentagon and the blue coloured region is its interior.

Note: A circle is not a polygon. Some students might think that if we increase the number of sides to infinity, we will get a circle which will be a polygon. But this thought is wrong as a polygon is a closed figure which has a finite number of sides. So, a circle cannot be a polygon.