Question

Draw a neat and labeled energy level diagram and explain the Balmer series and Brackett series of spectral lines for hydrogen atoms
The work function for a metal surface is 2.2 eV. If light of wavelength $5000\overset {\circ} {\mathop{A}}\, $ is incident on the surface of the metal, find the threshold frequency and incident frequency. Will there be an emission of photoelectrons or not? ($c=3\times {{10}^{8}}\dfrac{m}{s},1eV=1.6\times {{10}^{-19}},h=6.63\times {{10}^{-34}}J.s.$ ).

Answer 1

Hint: We will draw the energy level diagram of the hydrogen atom and locate different energy levels in it. From this respective diagram we are going to explain the blamer and brackett series of spectral lines. In the numerical we are going to find threshold frequency and for this we need to find work function and then, incident frequency.

Complete step-by-step answer:
First part: In the energy level of hydrogen atom, there are 5 energy states:
1) Lyman ; 2) Balmer ; 3) Paschen ; 4) Brackett ; 5) Pfund
These all energy states have different energies.
The figure given below is the energy level diagram of hydrogen atom:

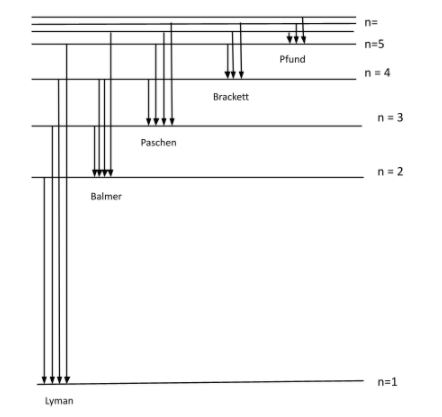
     The radiation associated with the transition can be categorized as, ultraviolet, visible and invisible spectrum of radiation.
We can see in the figure above and say that:
Balmer series: It is a series of spectral lines of energy where transition occurs from ${{n}_{i}}=2$ to ${{n}_{0}}=3,4,5,.......$
Its expression is written as –
$\dfrac{1}{\lambda }={{R}_{H}}\left[ \dfrac{1}{{{2}^{2}}}-\dfrac{1}{{{n}_{0}}^{2}} \right]$ ; ${{R}_{H}}$ =Rydberg’s constant
Brackett series: It is a series of spectral lines of energy where transition occurs from ${{n}_{i}}=4$ to ${{n}_{0}}=5,6,7,....$
Its expression is written as –
$\dfrac {1} {\lambda} = {{R} _ {H}}\left [ \dfrac{1}{{{4}^{2}}}-\dfrac{1}{{{n}_{0}}^{2}} \right]$
Second part:
We have already been provided that –
 $\begin {align}
  & work\, function= {{\phi} _ {0}} =2.2\, eV \\
 & =2.2\times 1.6\times {{10} ^ {-19}} J \\
 & =3.52\times {{10} ^ {-19}} J \\
\end{align}$
Now, as mentioned in question the values –
$\lambda =5000\overset {\circ} {\mathop{A}}\, $,
$\begin {align}
  & c=3\times {{10} ^ {8}}\dfrac {m} {s}, \\
 & h=6.63\times {{10} ^ {-34}} J.s. \\
\end{align}$
So, we will apply the formula of incident frequency (v) is –
$\therefore incident\, frequency (v) =\dfrac{c} {\lambda} $
$\begin {align}
  & =\dfrac {3\times {{10} ^ {8}}} {5\times {{10} ^ {-7}}} \\
 & =\dfrac {3} {5}\times {{10} ^ {15}}\, Hz \\
 & =\dfrac {30} {5}\times {{10} ^ {14\,}}\, Hz \\
 & =6\times {{10} ^ {14}}\, Hz \\
\end{align}$
And, the formula for threshold frequency (v0) is, ${{v} _ {0}} =\dfrac {{{\phi} _ {0}}} {h} $
$\begin {align}
  & \therefore {{v}_{0}}=\dfrac{3.52\times {{10} ^ {-19}} J} {6.63\times {{10} ^ {-34}} Js} \\
 & \,\,\,\,\,\,\,\,\,=0.53\times {{10} ^ {15}} Hz \\
 & \,\,\,\,\,\,\,\,\,=5.3\times {{10} ^ {14}} Hz \\
\end{align}$
Yes, there will be emission of photoelectrons as incident frequency is greater than threshold frequency.

Note: The potential energy at $n=\infty $is zero as nucleus does not attracts electron so, electrons are free moving and hence, are unstable whereas, in lowest energy state $n=1$, the electrons are tightly bonded, as there is more attractive force between nucleus and electron, and are highly stable and also have negative potential energy.