Question

Draw a diagram showing stages (cases) of projection for artificial satellites.

Answer 1

Hint:There will be a total of 5 cases of projection of artificial satellites depending upon their velocity in the space. Each case will trace a different path of the satellite. These paths will vary between a circle, an ellipse, a parabola or a hyperbola.

Complete Step by Step Solution:
When artificial satellites are launched into space, they are provided a velocity with which they can reach a point above earth where the centripetal force required for their movement around earth will be provided by the earth’s gravitation. If it gets too far or too close to earth, its path will vary. Once the satellite reaches that point, it is given a velocity in a direction such that it moves around the earth, like it is supposed to move. We will call this velocity $v$ . The different cases of projection are determined by this velocity of the satellite.

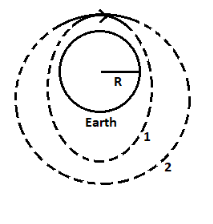
Case 1: $v < {v_o}$
Here, ${v_o}$ is called the orbital velocity. It is the velocity required by the satellite to undergo a circular trajectory around the earth. In other words, it is the velocity required by the satellite to undergo the path it is supposed to undergo.

In this case, the satellite will follow an elliptical path, very close to the earth.

Dotted line represents the path of the satellite in this case.

Case 2: $v = {v_o}$
In this case, the satellite will gain the velocity it was supposed to gain and will follow the path it was supposed to follow. It will trace a circular path.

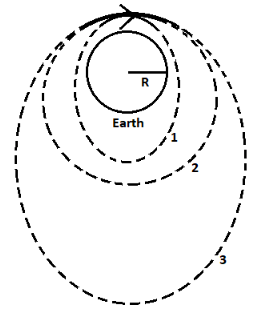
Case 3: ${v_o} < v < {v_e}$
Here, ${v_e}$ is the escape velocity. It is the velocity required by the satellite to escape the earth’s gravitational field. Once an object escapes earth’s gravitational field, it is not affected by its gravitation.
In this case too, the satellite will follow an elliptical path but not very close to the earth.

Case 4: $v = {v_e}$
In this case, the velocity of the satellite gets equal to the escape velocity. The satellite will escape the earth’s field of gravitation and will not return. It will follow a parabolic path.

Case 5: $v > {v_e}$
In this case too, the satellite will escape the earth’s gravitational field, but its path will be different. It will follow a hyperbolic path.

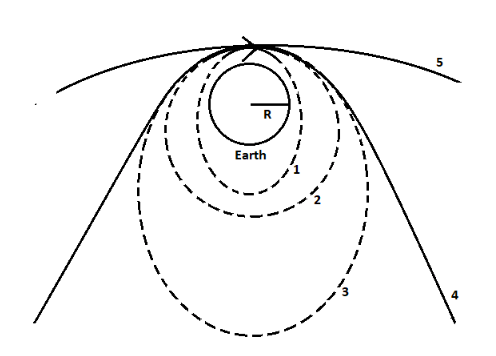
Note: In the last two cases, the satellite will leave the earth’s gravitational field after some time and hence their paths are not joined as it will not return. Lines on both left and right sides indicate the path if the direction of velocity was reversed. Joining the lines, however extended, will make the answer incorrect.