
Draw a circle of radius $3cm$
Draw triangle \[ABC\] with this circle as circumcircle and angle ${50^ \circ },{60^ \circ }$ and ${70^ \circ }$.
Construct triangle$PQR$, outside the circle, by drawing tangents to the circle at the points $A,B$and$C$.
Find all angles of triangle$PQR$
Answer
606.6k+ views
Hint: Use the necessary tools to attempt construction problems. Follow the construction steps.
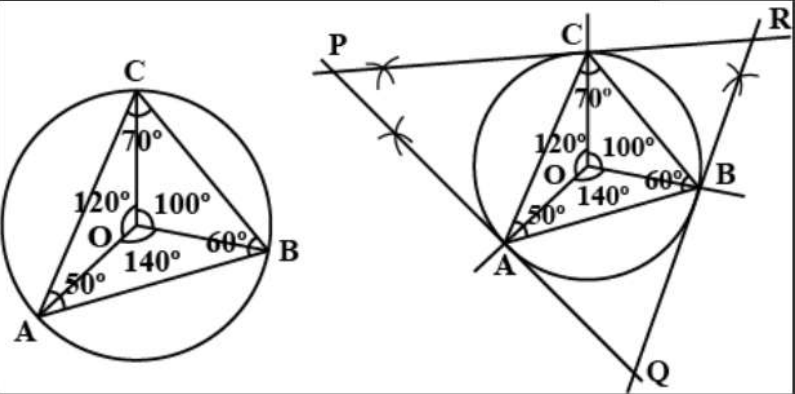
Step #1: Draw a circle with centre $O$ having radius \[3cm\].
Step #2: Take three points $A,B$and \[C\] in the circle and join \[A\] to the centre of the circle $O$.
Step #3: If \[\angle BAC\] is to be\[{50^ \circ }\], should be\[{100^ \circ }\].
Step #4: If \[\angle ABC\] is to be\[{60^ \circ }\], should be\[{120^ \circ }\].
Step #5: If \[\angle ACB\] is to be\[{70^ \circ }\], should be\[{140^ \circ }\].
Step #6: Join the points B and C such that \[m\angle AOC = {100^ \circ }\] and\[m\angle BOC = {120^ \circ }\].
Thus, \[\Delta ABC\]is the required triangle.
Step #1: Extend \[OA\] and draw perpendicular to it through\[A\].
Step #2: Extend \[OB\] and draw perpendicular to it through\[B\].
Step #3: In the same way draw a perpendicular from point \[C\] through\[OC\].
Let the points of intersection of these perpendicular be \[P,Q\] and\[R\], so we get the required \[\Delta PQR\].
\[m\angle AOC = {120^ \circ }\]
\[ \Rightarrow m\angle P = {180^ \circ } - {120^ \circ } = {60^ \circ }\] ……(opposite angles of a quadrilateral are supplementary)
In the same way,
\[ \Rightarrow m\angle Q = {180^ \circ } - {140^ \circ } = {40^ \circ }\]
And, \[ \Rightarrow m\angle R = {180^ \circ } - {100^ \circ } = {80^ \circ }\]
Note: Use the necessary tools to attempt construction problems. Mistakes can be made in reading the angles wrongly on the instruments or incorrect dimensioning in the diagram.
Steps of Construction:
Step #1: Draw a circle with centre $O$ having radius \[3cm\].
Step #2: Take three points $A,B$and \[C\] in the circle and join \[A\] to the centre of the circle $O$.
Step #3: If \[\angle BAC\] is to be\[{50^ \circ }\], should be\[{100^ \circ }\].
Step #4: If \[\angle ABC\] is to be\[{60^ \circ }\], should be\[{120^ \circ }\].
Step #5: If \[\angle ACB\] is to be\[{70^ \circ }\], should be\[{140^ \circ }\].
Step #6: Join the points B and C such that \[m\angle AOC = {100^ \circ }\] and\[m\angle BOC = {120^ \circ }\].
Thus, \[\Delta ABC\]is the required triangle.
Steps of Construction:
Step #1: Extend \[OA\] and draw perpendicular to it through\[A\].
Step #2: Extend \[OB\] and draw perpendicular to it through\[B\].
Step #3: In the same way draw a perpendicular from point \[C\] through\[OC\].
Let the points of intersection of these perpendicular be \[P,Q\] and\[R\], so we get the required \[\Delta PQR\].
In the quadrilateral \[PAOC\],
\[m\angle AOC = {120^ \circ }\]
\[ \Rightarrow m\angle P = {180^ \circ } - {120^ \circ } = {60^ \circ }\] ……(opposite angles of a quadrilateral are supplementary)
In the same way,
\[ \Rightarrow m\angle Q = {180^ \circ } - {140^ \circ } = {40^ \circ }\]
And, \[ \Rightarrow m\angle R = {180^ \circ } - {100^ \circ } = {80^ \circ }\]

Note: Use the necessary tools to attempt construction problems. Mistakes can be made in reading the angles wrongly on the instruments or incorrect dimensioning in the diagram.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




