Question

How does the area of the circle relate to the area of a parallelogram?

Answer 1

Hint: Here, we will first find the method of converting the geometrical figure parallelogram into a circle. Then by using the formula of the circumference of the circle, we will find the height and breadth of the parallelogram. We will then substitute these values in the formula of area of the Parallelogram to find the relation between the area of the circle and the area of the parallelogram is the required answer.

Formula Used:
We will use the following formula:
1. Area of a Parallelogram \[ = b \times h\] where \[b,h\] be the breadth and height of the Parallelogram.
2. Circumference of the circle \[ = 2\pi r\] where \[r\] is the radius of the circle.

Complete Step by Step Solution:
We have to find the relation between the area of the circle and the area of a parallelogram.
We know that when parallelogram is divided into smaller and further smaller segments which becomes into a number of rectangles.

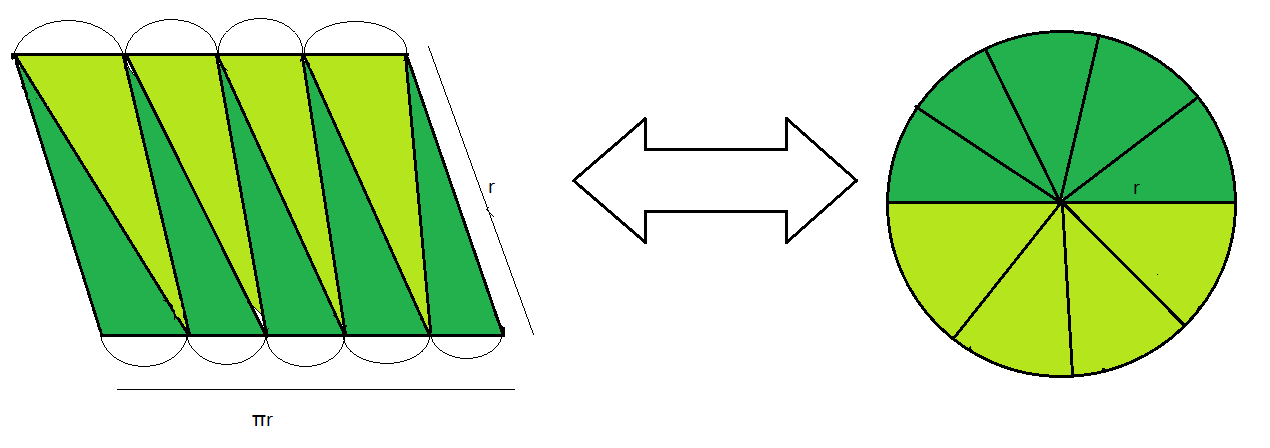
Thus, the smaller side of the Parallelogram is the radius of the circle and the longer side of the Parallelogram is the half of the circumference of the circle.
We know the Circumference of the circle \[ = 2\pi r\]. So,
Half the Circumference of the circle \[ = \dfrac{{2\pi r}}{2}\]
Dividing the terms, we get
\[ \Rightarrow \] Half the Circumference of the circle \[ = \pi r\]
Thus, the length of the Parallelogram is \[r\] and the breadth of the Parallelogram is \[\pi r\].
We know that Area of a Parallelogram \[ = b \times h\].
Substituting the values in the above formula, we get
Area of a Parallelogram \[ = \pi r \times r\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of a Parallelogram \[ = \pi {r^2}\]
So, we get the area of a Parallelogram \[\pi {r^2}\] which is equal to the area of the circle.
Therefore, if a circle is divided into a number of equal segments and arranged in a row from head to tail in an alternate manner, then we will get the resulting shape as a Parallelogram. It will have bulged sides on the breadth of the Parallelogram, this is because of the circle’s circumference.

So, the area of a Parallelogram will be the same as the area of the circle.

Note:
We know that a Parallelogram is a two dimensional geometrical figure whose sides are parallel to each other. Area of a Parallelogram is the region occupied by a Parallelogram in a two- dimensional Plane. Circle is a two dimensional curve whose distance from the center to any point on the curve is a constant which is called the radius of the circle. Area of a circle is the region occupied by a circle.