Question

What does a horizontal asymptote represent?

Answer 1

Hint: There are three different types of asymptotes: horizontal, vertical and oblique. In this question, we are going to discuss horizontal asymptotes. Generally, a horizontal asymptote is a horizontal line that represents the behavior of a function when the value of $ x $ is extremely small or large.

Complete step-by-step answer:
In this question, we are going to see what is horizontal asymptote, its examples and what it represents. First of all, let us see what horizontal asymptote is.
When a rational function is given, you might notice those horizontal lines. These lines are known as the horizontal asymptotes of the function. If we know their values, we can understand the function’s restricted values.
Horizontal asymptotes of the function helps us understand the behavior of function when the inputs are very small and large.
Horizontal Asymptote: Horizontal asymptote of a given function represents the values of $ f\left( x \right) $ , when $ x $ is significantly small or large.
Generally, the equations of horizontal asymptote are represented by $ y = a $ , where $ a $ is the value of $ y $ when $ x \to \pm \infty $ .
They are represented by horizontal lines and most of the time they are represented by dashed lines.
We can find the horizontal asymptote of a function by determining the function’s restricted output values. Horizontal asymptote is simply the value of $ \mathop {\lim }\limits_{x \to \infty } f\left( x \right) $ .
Let us take an example and draw a graph for the horizontal asymptote.

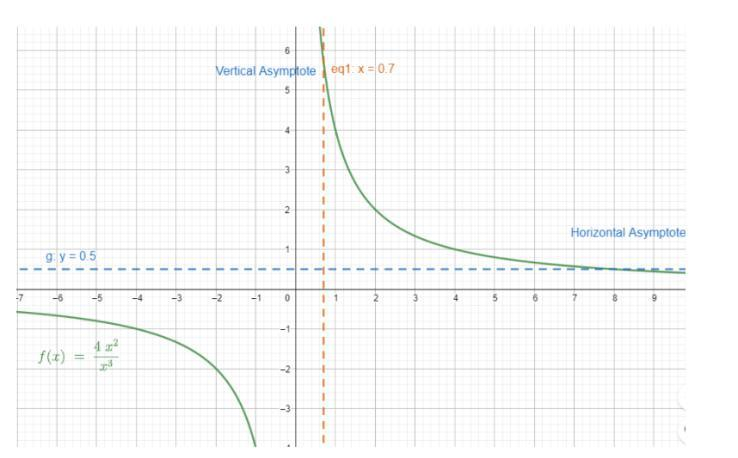
In the above graph, $ f\left( x \right) = \dfrac{{4{x^3}}}{{{x^2}}} $ and line $ y = 0.5 $ shows us the horizontal asymptote and the line $ x = 0.7 $ shows the vertical asymptote.

Note: The difference between vertical asymptote and horizontal asymptote is that a function’s curve can never pass through its vertical asymptote but it can pass through its horizontal asymptote. Also, vertical asymptotes are the vertical lines near which the function grows without bound.