Question

Director Circle of parabola \[{\left( {x - 2} \right)^2} = 16\left( {y + 7} \right)\] touches the circle ${\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = {r^2}$ then ${r^2}$ is:
A) \[12\]
B) \[144\;\]
C) \[10\;\]
D) \[100\]

Answer 1

Hint: In the conic section the director circle of a parabola \[{\left( {x - 2} \right)^2} = 16\left( {y + 7} \right)\] is the directrix of the curve. In this problem first we consider the terms $\left( {x - 2} \right)$ as X and $\left( {y + 7} \right)$ as Y. and the equation so formed compare with ${x^2} = 4ay$ and by this we find the value of a. Then we use the general equation of the directrix of a parabola $y + a = 0$ for getting the equation of the directrix of the given parabola.
Given a circle touches ${\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = {r^2}$ the directrix of given parabola so it becomes tangent of parabola therefore we find the perpendicular distance of this directrix from the center of the circle. The perpendicular distance is the radius of the given circle. by taking the square of radius ${r^2}$ we get the required answer.

Complete step by step solution:
Given parabola \[{\left( {x - 2} \right)^2} = 16\left( {y + 7} \right)\]
Let us consider the terms $\left( {x - 2} \right)$ as X and $\left( {y + 7} \right)$ as Y.
Then the given parabola become
${X^2} = 16Y$ ----------------(1)
We compare equation (1) with the general equation of parabola i.e. ${x^2} = 4ay$
On comparing this we get
$
  4a = 16 \\
   \Rightarrow a = \dfrac{{16}}{4} \\
   \Rightarrow a = 4 \\
 $
Since, the general equation of directrix of parabola ${x^2} = 4ay$ is $y + a = 0$
By using this equation we get the equation of directrix of given parabola
$Y + 4 = 0$
Now on putting $Y$ as $\left( {y + 7} \right)$ , we get
$y + 7 + 4 = 0$
$ \Rightarrow y + 11 = 0$ ------------- (2)
Given, the circle equation is ${\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = {r^2}$.
On comparing the above equation with the general equation of circle ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$ whose center is $\left( {h,k} \right)$
We get the center of the given circle which will be C $\left( { - 1,1} \right)$.
Since the directrix of a given parabola is tangent on this circle.
Now, we can draw a graph for the given parabola and center of circle.

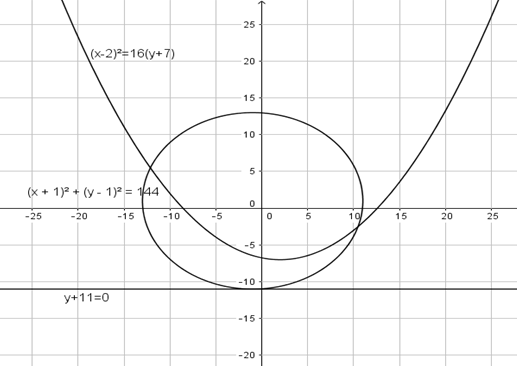
So we find the perpendicular distance of directrix [equation (2)] from the center of the circle C $\left( { - 1,1} \right)$. This perpendicular distance is the radius of the circle.
$
  r = \left| {\dfrac{{1 + 11}}{{\sqrt {{1^2}} }}} \right| \\
   \Rightarrow r = \left| {\dfrac{{12}}{1}} \right| \\
   \Rightarrow r = 12 \\
 $
Therefore the radius ($r$) of the circle is $12$ unit.
On taking square of ‘$r$’ we get the value of ${r^2}$
$
  {r^2} = {\left( {12} \right)^2} \\
   \Rightarrow {r^2} = 144 \\
 $
Therefore, Director Circle of parabola \[{\left( {x - 2} \right)^2} = 16\left( {y + 7} \right)\] touches the circle ${\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} = {r^2}$ then ${r^2}$ is \[144\]. Hence the correct answer is option (B).

Note:
> The use of the general form equation of curves and related terms in the general form is often a critical part of the solution in the conic section.
> We were supposed to find the equation of the director circle in this question, but instead we got the equation of the directrix, which is a straight line.
> In this case, a straight line is represented by a circle with an infinite diameter.
> The equation of the director circle is in the form of a circle, not a straight line, for curves like ellipse and hyperbola.