Dinesh went from place A to place B and from there to place C. A is 7.5km from B and B is 12.7km from C. Ayub went from place A to place D and from there to place C. D is 9.3km from A and C is 11.8km from D. Who travelled more and by how much ?
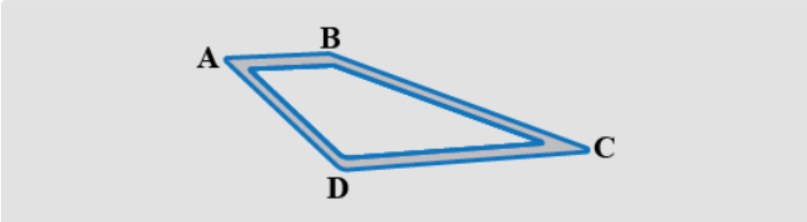
Hint: Use the information given in the question to find out the lengths of the different sides that make up the trapezium ABCD. Then, sum up the lengths as directed for each person to know who travelled more.
Answer
Verified364.5k+ views
First, let’s find out the lengths of the individual sides of the trapezium as shown. Let’s go line by line in the question.
We know that is 7.5km from .
Therefore, this means that = 7.5km.
Next, it is written that is 12.7km from .
Therefore, this means that = 12.7km.
Next, we have that is 9.3km from .
Therefore, this means that = 9.3km.
Lastly, we have that is 11.8km from .
Therefore, this means that = 11.8km.
Hence, we have the measurements of each side of the trapezium given to us. We now know that,
is a trapezium, where :
= 7.5km, = 12.7km, = 11.8km, and = 9.3km.
Now, let’s analyse the paths each person took while travelling.
First, let’s calculate the distance travelled by Dinesh. It is said, that he travels from , to , to . Therefore, the distance Dinesh covered = length of + length of =
Next, let’s calculate the distance covered by Ayub. It is written that Ayub went from place , to , to .
Therefore, Ayub covered a distance = length of + length of =
Hence, we now have the distances covered by both, Dinesh and Ayub, to compare the distances they travelled and to tell who travelled more.
Ayub covered 21.2km while Dinesh covered 20.2km. We can clearly see, that Ayub covered more distance than Dinesh. The path that was extra covered by him = .
Hence, Ayub travelled more, and by 1km.
Note: There are no properties of trapezoids being used in this question. In case we had been given the distance between two opposite corners of the trapezium, or we knew that the trapezoid was an isosceles trapezium, then we could have made use of some property of special trapezoids. However, this is a very straightforward question. You need to be very careful about mentioning the units of the distances and the calculation, since so much data might confuse you.
We know that is 7.5km from .
Therefore, this means that = 7.5km.
Next, it is written that is 12.7km from .
Therefore, this means that = 12.7km.
Next, we have that is 9.3km from .
Therefore, this means that = 9.3km.
Lastly, we have that is 11.8km from .
Therefore, this means that = 11.8km.
Hence, we have the measurements of each side of the trapezium given to us. We now know that,
is a trapezium, where :
= 7.5km, = 12.7km, = 11.8km, and = 9.3km.
Now, let’s analyse the paths each person took while travelling.
First, let’s calculate the distance travelled by Dinesh. It is said, that he travels from , to , to . Therefore, the distance Dinesh covered = length of + length of =
Next, let’s calculate the distance covered by Ayub. It is written that Ayub went from place , to , to .
Therefore, Ayub covered a distance = length of + length of =
Hence, we now have the distances covered by both, Dinesh and Ayub, to compare the distances they travelled and to tell who travelled more.
Ayub covered 21.2km while Dinesh covered 20.2km. We can clearly see, that Ayub covered more distance than Dinesh. The path that was extra covered by him = .
Hence, Ayub travelled more, and by 1km.
Note: There are no properties of trapezoids being used in this question. In case we had been given the distance between two opposite corners of the trapezium, or we knew that the trapezoid was an isosceles trapezium, then we could have made use of some property of special trapezoids. However, this is a very straightforward question. You need to be very careful about mentioning the units of the distances and the calculation, since so much data might confuse you.
Last updated date: 20th Sep 2023
•
Total views: 364.5k
•
Views today: 8.64k
