Question

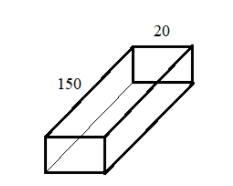
Diagram shows a rectangular trough of length \[150cm\]and width \[20cm\]. The trough was completely filled with \[48000c{m^3}\]of water from the tank. Calculate the depth of the trough.

Answer 1

Hint: The given diagram is cuboid. We need to know some properties and formulae of cuboids.
3D-shape of the rectangle is cuboid. It has six faces, four rectangles and two square faces.
Volume of a cuboid is given by \[l \times b \times h\] where \[l\]is the length of the cuboid, \[b\]is the breadth of the cuboid and \[h\]is the height of the cuboid. Height is nothing but the depth of the cuboid.

Complete step by step answer:
It is given that there is a cuboid of length \[150cm\]and width \[20cm\] filled with \[48000c{m^3}\]of water fully. Thus, this amount of water is nothing but the volume of the cuboid.
We know that, volume of a cuboid is given by, \[l \times b \times h\] where \[l\]is the length of the cuboid, \[b\]is the breadth of the cuboid and \[h\]is the height of the cuboid.
We already have \[l = 150cm\],\[b = 20cm\]and \[V = 48000c{m^3}\]. Let us substitute these in the volume formula.
\[V = l \times b \times h \Rightarrow 48000 = 150 \times 20 \times h\]
Our aim is to find the depth that is the height of the cuboid.
On simplifying the above expression, we get
\[ \Rightarrow 48000 = 3000 \times h\]
On further simplification,
\[ \Rightarrow h = \frac{{48000}}{{3000}}\]
Let’s simplify it again. We get,
\[ \Rightarrow h = 16\]
Thus, we got the value of \[h\]as \[16cm\]. Since height is nothing but the depth of the cuboid we get, the depth of the given diagram is \[16cm\].

Note: Height of the cuboid is also known as depth of a cuboid. Since we know the volume, length and breadth, we used the volume formula to find the value of height. We cannot use the area formula to find the height of the cuboid since it doesn’t contain the term height. Volume is the only formula that contains the term height thus, we used that formula also we had the value of volume which made the calculation simpler.