Question

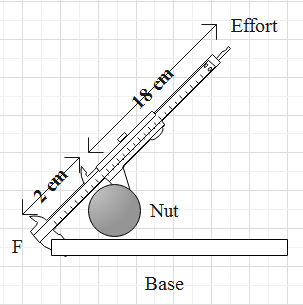
Diagram alongside shows a nut-cracker with a wooden base. If the effort required to crack the nut is 50 N, find the resistance offered by the nut.

Answer 1

Hint: Using the free body diagrams for both, the nut and the nut-cracker becomes easy to determine the number of forces acting on the both. Upon determining the forces, we can equate them and find the resistance offered by the nut. The force exerted by the nut-cracker should be equated to the resistance offered by the nut.

Formula used:
\[{{E}_{a}}\times E={{L}_{a}}\times L\]

Complete step-by-step answer:
There are two methods to solve this problem. They are, one is a formula method and the other one is a free body diagram method.

The formula used to calculate the resistance offered by the nut is given as follows.
\[{{E}_{a}}\times E={{L}_{a}}\times L\]

From the diagram, the data derived is as follows.
The effort required to crack the nut, \[E=50\,N\]
The effort arm, \[{{E}_{a}}=18+2=20\,cm\]
\[{{E}_{a}}=0.2m\]
The load offered by the nut, \[L\]
The load arm, \[{{L}_{a}}=2\,cm\]
\[{{L}_{a}}=0.02m\]

Now substitute these values in the above formula provided. Thus, we get,
\[\begin{align}
  & 20\times 50=2\times L \\
 & \Rightarrow L=\dfrac{20\times 50}{2} \\
 & \Rightarrow L=500\,N \\
\end{align}\]

Therefore, the resistance offered by the nut, for the effort required to crack the nut by 50 N is 500 N.

The FBD of the nut and nut-cracker

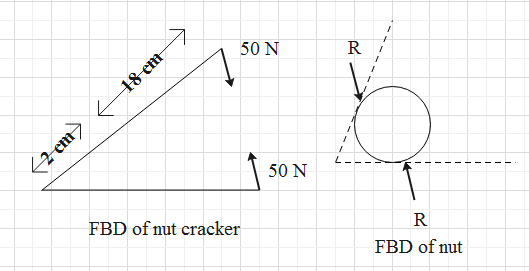
The torque about the end point of the nutcracker is,

\[\begin{align}
  & R\times 2=50\times (18+2) \\
 & \Rightarrow R=\dfrac{50\times 20}{2} \\
 & \Rightarrow R=500\,N \\
\end{align}\]

Therefore, the resistance offered by the nut, for the effort required to crack the nut by 50 N is 500 N.

Note: This concept is completely based on Newton’s third law of motion. For the action of the nut-cracker, the reaction, that is resistance will be offered by the nut. Instead of the resistance offered by the nut, the force applied by the nut-cracker can be asked. The units of the parameters should be taken care of. Here, the force is given in Newton, so we have found the resistance in terms of Newton.