Question

How do you determine the interval(s) over which f(x) is increasing, decreasing, constant, concave up, concave down? What are the zeros of the f(x)? For what values of x, f(x) is discontinuous?

Answer 1

Hint: This type of problem is based on the concept of maxima and minima of a function. First, we have to differentiate the given function. If the sign of the derivative is positive, then the function is increasing and if it is negative, the function is decreasing. If the derivative is equal to 0 in the whole interval, then the function is constant. To find whether the function is concave up or concave down, we have to find the second derivative. If it is positive, then f(x) is concave up. To find the zeros of the function f(x), we have to equate f(x)=0 and find the values of x.

Complete step-by-step solution:
According to the question, we have to find whether the function is increasing, decreasing, constant, concave up or concave down. Then, we have to find the zeros of the function and check whether the function is continuous or not.
Let us assume that \[f\left( x \right)={{x}^{2}}\].
Let us first differentiate f(x) with respect to x.
\[\Rightarrow \dfrac{d}{dx}f\left( x \right)=\dfrac{d}{dx}\left( {{x}^{2}} \right)\]
Using the power rule of differentiation \[\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}\], we get
\[\dfrac{d}{dx}f\left( x \right)=2{{x}^{2-1}}\]
On further simplification, we get
\[{f}'\left( x \right)=2x\]
Here we find that the derivative of f(x) is 2x
When x>0, we get \[{f}'\left( x \right)>0\]. That is the derivative is positive.
Therefore, the function f(x) is increasing when x>0.
When x<0, we get \[{f}'\left( x \right)<0\]. That is, the derivative is negative.
Therefore, the function f(x) is decreasing when x<0.
Let us plot a graph for clarification.

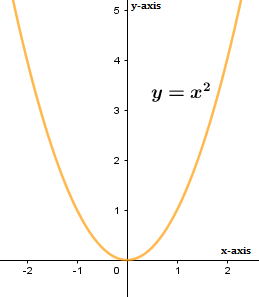
We can clearly understand that f(x) is increasing for x>0 and decreasing for x<0.
Now, we have to find whether the function is concave up or down. Let us find the second derivative of f(x).
\[\dfrac{d}{dx}\left( {f}'\left( x \right) \right)=\dfrac{d}{dx}\left( 2x \right)\]
\[\Rightarrow \dfrac{d}{dx}\left( {f}'\left( x \right) \right)=2\dfrac{dx}{dx}\]
We know that \[\dfrac{dx}{dx}=1\]. Therefore, we get
\[{f}''\left( x \right)=2\]
Here, we find that the second derivative of f(x) is positive.
Thus, we get the function concave up.
And we can clearly understand from the graph as well.
Now, we have to find the zeros of the function f(x).
To find the zeros of the function, we have to equate f(x) equal to 0.
\[\Rightarrow f\left( x \right)=0\]
\[\Rightarrow {{x}^{2}}=0\]
On taking square root on both the sides of the equation, we get
\[\sqrt{{{x}^{2}}}=\sqrt{0}\]
We know that \[\sqrt{{{x}^{2}}}=\pm x\]. Therefore, we get
\[x=\pm 0\]
\[x=0\]
Thus the zeros of f(x) is x=0.
We can clearly find from the graph that the function is continuous at all the points.
Thus the function has no point of discontinuity.
Therefore, the function f(x) is continuous and is zero at x=0. The function is decreasing when x=0 and increasing when x>0.

Note: We should be very careful with the differentiation. Avoid calculation mistakes based on sign conventions. It is advisable to plot the graph of the given function to get more clarification for the answer.