Question

Describe the principle and working of a meter bridge?

Answer 1

Hint
The principle behind the meter bridge is the formation of a Wheatstone bridge. It is known that when a Wheatstone bridge is formed, no current flows through the middle resistor, thus in a meter bridge a galvanometer is situated in the middle and when the reading becomes zero, the value of the unknown resistor can be found.

Complete step by step answer
As discussed in the hint, a meter bridge works on the principle of a Wheatstone bridge.
A meter bridge consists of a $ 1m $ long resistor wire. It is made of resistive material like manganin or constantan, it also has a uniform cross-section throughout its length, so that the resistance offered by the wire only depends on the length of the wire. The wire connecting the galvanometer is touched using a jockey and slid along this wire which divides the meter wire into two parts, both of which act as two of the resistors of Wheatstone bridge.
Another known resistor (from a resistance box) is used as a third resistor of a Wheatstone bridge, while the fourth is the unknown resistance.
The length at which the reading of the galvanometer becomes zero is used to calculate the resistance of the resistor wire. And these three resistance values can be used to calculate the value of the fourth unknown resistor.

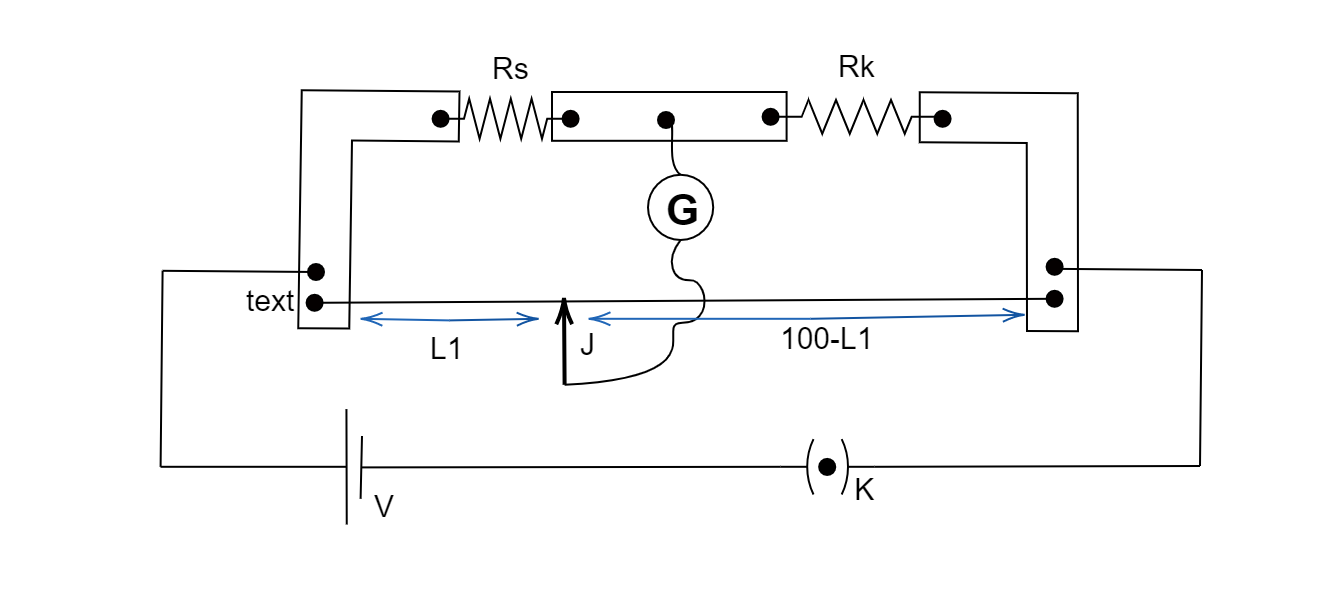
Assume that the reading of galvanometer (G) becomes zero at the length $ {L_1} $ of the resistor wire, then the other length $ {L_2} $ can be related as:
 $ \Rightarrow {L_1} + {L_2} = 100 $ (in cm)
Therefore, $ {L_1} = 100 - {L_1} $
The resistance of the wire is given by,
 $ \Rightarrow {R_L} = \dfrac{{\rho L}}{A} = \left( {\dfrac{\rho }{{\pi {r^2}}}} \right) \times L = KL $
The term $ \dfrac{\rho }{{\pi {r^2}}} $ is a constant denoted by K, which is calculated beforehand, here $ \rho $ is the specific resistance of the material, and r is the radius.
Therefore,
 $ \Rightarrow {R_{L1}} = K{L_1} $
 $ \Rightarrow {R_{L2}} = K(100 - {L_1}) $
Let $ {R_k} $ be the known resistance, then the Wheatstone bridge formula is :
 $ \Rightarrow {R_s} \times (100 - {L_1}) = {R_K} \times {L_1} $
Therefore, the unknown resistance $ {R_s} $ is given by,
 $ \Rightarrow {R_S} = \left( {\dfrac{{{L_1}}}{{100 - {L_1}}}} \right) \times {R_K} $

Note
The value of $ K $ is not necessary to calculate to get the value of $ {R_S} $ because it gets canceled out in the process of multiplying the Wheatstone resistors. Therefore only values of $ {L_1} $ and $ {R_k} $ are needed.