Question

Derive expression for the self-induction of solenoid. What factors affect its value and how?

Answer 1

Hint: Find the magnetic flux linked with the solenoid. Assume the solenoid to be very long, and the magnetic flux to be uniform inside at each point. Then find the self-inductance of the solenoid, where there is a substance of relative permeability instead of air or vacuum.

Complete step by step answer:

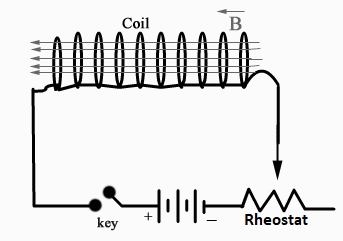
Here in the diagram, we see a coil in which current is passed with the help of a DC source, and a rheostat to control the current supplied, we see that the direction of current supplied is totally opposite to the magnetic flux induced in the coil.
Self Inductance of a Current-Carrying Solenoid: Consider a solenoid of radius r meter, length l meter, having a total number of turns N and carrying a current I ampere. The magnetic field produced on its axis inside the solenoid is
$B=\dfrac{{{\mu }_{0}}NI}{l}N{{A}^{-1}}{{m}^{-1}}$
If it is assumed that the solenoid is very long, the intensity of magnetic field B can be assumed to be uniform inside it at each point, then the total magnetic flux linked with the solenoid is
$B=\dfrac{{{\mu }_{0}}m}{4\pi }[\dfrac{{{d}^{2}}+{{l}^{2}}+2dl-({{d}^{2}}+{{l}^{2}}-2dl)}{{{\{(d-l)(d+l)\}}^{2}}}]$
$\phi =B\times $Total effective area of the solenoid.
$=B\times (NA)$
Where $A=\pi {{r}^{2}}$ is the area of the cross section of solenoid.
$\therefore \quad \quad \phi =\dfrac{{{\mu }_{0}}NI}{l}\times NA=\dfrac{{{\mu }_{0}}{{N}^{2}}AI}{l}$weber.
But by definition ϕ=LI where L is the self-inductance of the solenoid, therefore
$L=\dfrac{\phi }{I}=\dfrac{{{\mu }_{0}}{{N}^{2}}A}{l}$henry,
If inside the solenoid instead of air or vacuum there is a substance of relative permeability
$L=\dfrac{{{\mu }_{0}}{{\mu }_{r}}{{N}^{2}}A}{l}$
Thus, the self-inductance of a solenoid depends on the following factors:
(i) The self-inductance increases on increasing the number of turns, which means it depends on the number of turns in the coil of the solenoid.
(ii) The self-inductance increases on increasing the area of cross-section, which means it depends on the area of cross-section or radius of the solenoid.
(iii) On increasing the length of solenoid, its self-inductance decreases.
(iv) If a soft iron rod is placed inside the solenoid, its self-inductance increases, which means it depends on the relative permeability of the substance placed inside the solenoid.
We have to remember that if the number of turns per unit length of the solenoid is n, then n=N/l and the self-inductance of the solenoid is,
$L={{\mu }_{0}}{{n}^{2}}lA$

Note: Consider the magnetic field to be uniform throughout the solenoid. Remember to find the solution within the medium of relative permeability.Larger the length of the solenoid lesser is its self-inductance.