Question

Derive $ \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u} $ formula for spherical mirror.

Answer 1

Hint :First, for any finite position of the object, draw the ray diagram and provide the general Cartesian sign conventions. Now, for the triangles obtained from the pole and centre of curvature with the object and image, we apply the similar triangles rule. The equations obtained would be in the form of a radius of curvature which can be converted to focal length when the object is considered to be formed at infinity.

Complete Step By Step Answer:
The formula for a spherical mirror which relates the focal length, image distance and the object distance is known as mirror formula.

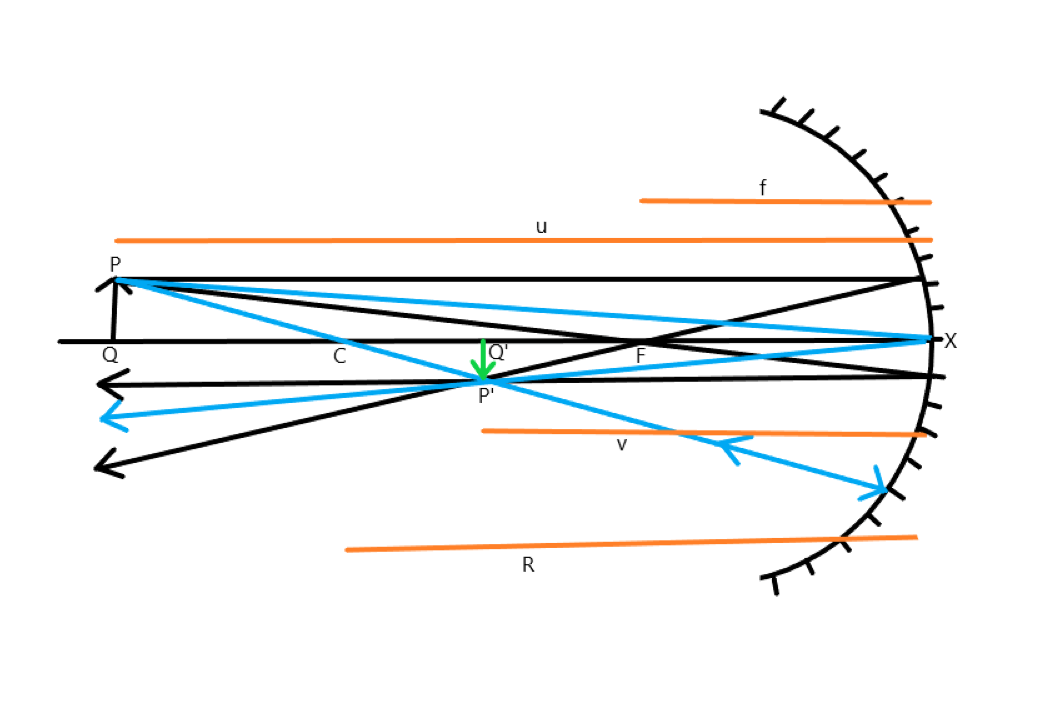
Here, we consider a concave mirror, the object is PQ and its image is P’Q’. According to the Cartesian sign convention, let the object distance XQ be u, such that XQ=-u. The image distance XQ’ is v such that XQ’=-v. The focal length f of the mirror is XF=-f. Here, XC is the radius of curvature, where XC=-R.
Now, from the above figure, it can be clearly seen that $ \Delta PQX\& \Delta P'Q'X $ are similar triangles. Thus,
 $
  \dfrac{{P'Q'}}{{PQ}} = \dfrac{{XQ'}}{{XQ}} = \dfrac{{ - v}}{{ - u}} \\
  \dfrac{{P'Q'}}{{PQ}} = \dfrac{v}{u} \\
  $
 Suppose the above is equation (1). Now, in a similar way, $ \Delta PQC\& \Delta P'Q'C $ are similar triangles. Thus,
 $
  \dfrac{{P'Q'}}{{PQ}} = \dfrac{{CQ'}}{{CQ}} \\
    \\
  $
Let above equation be equation (2). Now, from the figure,
 $
  CQ' = CX - XQ' = - R - ( - v) = - R + v \\
  CQ = XQ - XC = - u - ( - R) = - u + R \\
  $
 Substituting above equations in equation (2), we get,
 $ \dfrac{{P'Q'}}{{PQ}} = \dfrac{{CQ'}}{{CQ}} = \dfrac{{ - R + v}}{{ - u + R}} $
Let this be equation (3). Comparing equation (1) and (3), we get,
 $
  \dfrac{v}{u} = \dfrac{{ - R + v}}{{ - u + R}} \\
   - uv + Rv = - Ru + vu \\
  Rv + Ru = 2uv \\
  R(u + v) = 2uv \\
  \therefore \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{2}{R} \\
  $
Now, when the object is at a distance close of infinity, its image will be at the principle focus. Thus,
  $
  \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{2}{R} \\
  \dfrac{1}{f} + \dfrac{1}{\infty } = \dfrac{2}{R} \\
  \dfrac{1}{f} = \dfrac{2}{R} \\
  $
Thus, from this equation, we obtain the mirror formula as follows:
 $ \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u} $ $ $
Hence the formula is proved.

Note :
 This formula is applicable for both the types of spherical mirrors and for all the positions of the objects. From this formula, we can obtain the position of the image, object as well as the focal length of the object, but we cannot obtain what kind of image is formed through this formula only, unless we know the type of mirror used.