Question

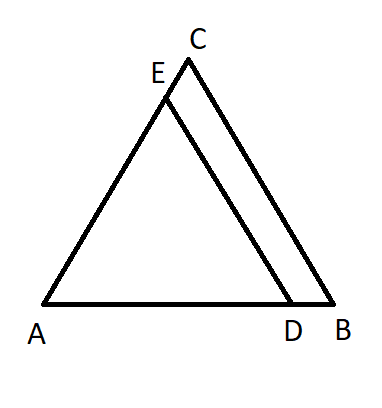
\[DE\parallel BC\], If \[AD=x,DB=x-2,AE=x+2,EC=x-1\] find the value of x.

Answer 1

Hint: In this problem, we have to find the value of x from the given triangle ABC. We are given that the line DE is parallel to BC. We are also given that we can use Thales Theorem and substitute the given value in the fraction to find the value of x.

Complete step by step answer:
We know that the given triangle ABC, where the line DE is parallel to BC, \[DE\parallel BC\].

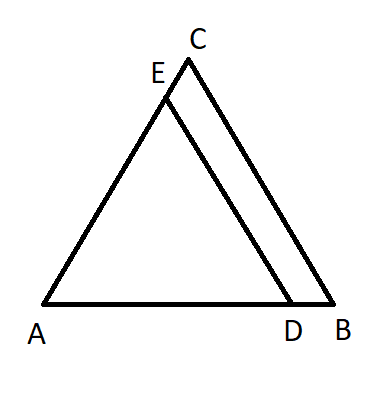
We know that the Thales Theorem from the diagram whose line DE is parallel to BC is,
\[\dfrac{AD}{DB}=\dfrac{AE}{EC}\]
We can write the above theorem as,
\[AD\times EC=AE\times DB\]
 We know that the given values are, \[AD=x,DB=x-2,AE=x+2,EC=x-1\].
We can substitute these values in the above theorem, we get
\[\Rightarrow x\times \left( x-1 \right)=\left( x+2 \right)\times \left( x-2 \right)\]
We can multiply the term in the left-hand side and we can use the algebraic formula in the right-hand side, we get
\[\Rightarrow {{x}^{2}}-x={{x}^{2}}-4\]
Now we can cancel similar terms in both the left-hand side and the right-hand side in the above step, we get
\[\Rightarrow -x=-4\]
Now we can multiply -1 on both the left-hand side and the right-hand side in the above step, we get
\[\Rightarrow x=4\]

Therefore, the value of x is 4.

Note: Students make mistakes while writing the Thales theorem form the given diagram, which should be concentrated. To solve this problem, we have to understand the concept of Thales theorem to be used. We should go through the question properly, in order to find what should be taken from the question.