
Degree of freedom of a triatomic gas is? (Consider moderate temperature)
A. 6
B. 4
C. 2
D. 8
Answer
579.9k+ views
Hint: Degree of freedom is the number of independent motions a particle can undergo. To find out the degree of freedom we have to find the number of independent motions possible for that particular molecule. Here we have a triatomic gas and in order to find its degree of freedom, we check its possible motions in x, y and z directions.
Complete step by step answer:
We have to find the Degree of freedom of a triatomic molecule. A triatomic gas molecule has 3 atoms in it.
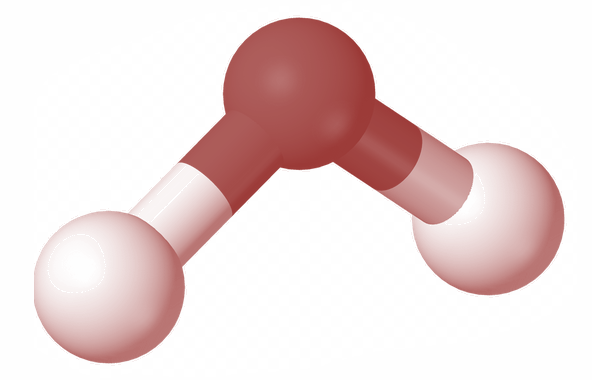
Consider a triatomic gas molecule as shown in the figure above.
We now consider the possible movements of this molecule in the x, y and z axis.
Here this triatomic gas can have a translatory motion along the x, y, and z axis. I.e. triatomic molecules can move along x direction, y direction and z direction.
Hence the translatory degree of freedom of this molecule is 3
Now let us consider the rotational degree of freedom of this molecule.
For that we place two atoms of the molecule on the x axis. Then it can rotate about y axis and z axis. It also has a significant rotation about x axis because here the third atom has a moment of inertia about x axis even if the other two atoms do not have the inertia.
And thus the rotational degree of freedom of this molecule is also three.
Hence the degree of freedom= Translatory degree of freedom + Rotational degree of freedom
=3+3=6
Therefore at moderate temperature the degree of freedom of a triatomic gas equals to 6.
So, the correct answer is “Option A”.
Note: We can also find the degree of freedom by using the general expression
Degree of freedom, $\text{DF=3N-n}$ where N is the total number of particles and n is holonomic constraints.
We have a triatomic molecule. And hence the number of particles, $\text{N=3}$. And since the separation between 3 atoms is fixed, the number of holonomic constraints, $\text{n=3}$.
Therefore we have,
$\begin{align}
& \text{DF=3 }\!\!\times\!\!\text{ 3 - 3} \\
& \text{DF=9 - 3} \\
& \text{DF=6} \\
\end{align}$
Thus the degree of freedom of a triatomic molecule is 6.
Complete step by step answer:
We have to find the Degree of freedom of a triatomic molecule. A triatomic gas molecule has 3 atoms in it.
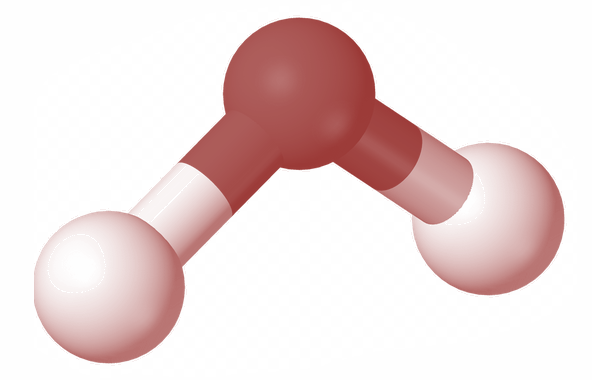
Consider a triatomic gas molecule as shown in the figure above.
We now consider the possible movements of this molecule in the x, y and z axis.
Here this triatomic gas can have a translatory motion along the x, y, and z axis. I.e. triatomic molecules can move along x direction, y direction and z direction.
Hence the translatory degree of freedom of this molecule is 3
Now let us consider the rotational degree of freedom of this molecule.
For that we place two atoms of the molecule on the x axis. Then it can rotate about y axis and z axis. It also has a significant rotation about x axis because here the third atom has a moment of inertia about x axis even if the other two atoms do not have the inertia.
And thus the rotational degree of freedom of this molecule is also three.
Hence the degree of freedom= Translatory degree of freedom + Rotational degree of freedom
=3+3=6
Therefore at moderate temperature the degree of freedom of a triatomic gas equals to 6.
So, the correct answer is “Option A”.
Note: We can also find the degree of freedom by using the general expression
Degree of freedom, $\text{DF=3N-n}$ where N is the total number of particles and n is holonomic constraints.
We have a triatomic molecule. And hence the number of particles, $\text{N=3}$. And since the separation between 3 atoms is fixed, the number of holonomic constraints, $\text{n=3}$.
Therefore we have,
$\begin{align}
& \text{DF=3 }\!\!\times\!\!\text{ 3 - 3} \\
& \text{DF=9 - 3} \\
& \text{DF=6} \\
\end{align}$
Thus the degree of freedom of a triatomic molecule is 6.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




