Question

Define relaxation time of the free electrons drifting in a conductor: How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.

Answer 1

Hint: Drift velocity is directly proportional to relaxation time. Write the formula for current flowing through the conductor. Substitute the value of drift velocity in terms of relaxation time. Use the formula for electric field applied and Ohm’s law. Get the value of R in terms of l and A.

Formula used:
${ v }_{ d } = -\dfrac { eE }{ m } \tau $
$I = -neA{ v }_{ d }$
$V = IR$

Complete step by step answer:
Relaxation time is defined as the time interval between two successive collisions of electrons in a conductor when current flows through it. It is denoted by $ \tau$.
Relation between drift velocity of the electrons (${ v }_{ d }$) and relaxation time (\tau) is given by,
${ v }_{ d } = -\dfrac { eE }{ m } \tau$ …(1)
Where, E: Electric field
            M: mass of electron
             E: charge of electron

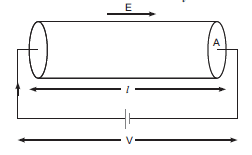
Consider a conductor having length l, area of cross section A and current density n.
Current flowing through the conductor is given by,
$I = -neA{ v }_{ d }$…(2)
Now, by substituting equation.(1) in equation.(2) we get,
$I = neA\dfrac { eE }{ m } \tau$
$\therefore I = \dfrac { n{ e }^{ 2 }AE }{ m } \tau$ …(3)
Electric field applied is given by,
$E = \dfrac { V }{ l }$ …(4)
Substituting equation. (3) in equation.(4) gives,
$I =\dfrac { n{ e }^{ 2 }AV\tau }{ ml }$
Now, by rearranging the equation we get,
$\dfrac { V }{ I } = \dfrac { ml }{ n{ e }^{ 2 }A\tau }$ …(5)
According to Ohm’s Law,
$V = IR$
Rearranging the above equation we get,
$R = \dfrac { V }{ I }$
Now, substituting the equation. (5) in above equation we get,
$R = \dfrac { ml }{ n{ e }^{ 2 }A\tau }$
Let $\rho = \dfrac { m }{ n{ e }^{ 2 }\tau }$
$\therefore R = \rho \dfrac { l }{ A }$
Where, $\rho$ : Resistivity of the material
Therefore, the expression for electrical resistivity is given by $\rho = \dfrac { m }{ n{ e }^{ 2 }\tau }$.

Note:
Electrical resistivity is inversely proportional to relaxation time. Reciprocal resistivity gives conductivity. It is denoted by $\sigma$. Therefore, $\sigma = \dfrac { n{ e }^{ 2 }\tau }{ m }$.
As the temperature of the conductor is decreased, the number of electron collisions also decreases. As a result, relaxation time gets increased. Thus we can say, relaxation time is dependent on temperature.