Question

Define constant function. Also write its graph. Domain and range of function.

Answer 1

Hint: A function is a rule which relates the values of one variable quantity to the values of another variable quantity.

Complete step by step solution: A constant function is a function whose (output) value is the same for every input value.
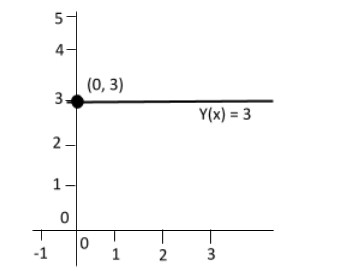
For example, the function \[y\left( x \right) = {\text{3}}\] is a constant function because the value of \[y\left( x \right)\] is \[{\text{3}}\] regardless of the input value $ x $.
Domain of function: The domain of a function is the complete set of possible values of the independent variable.
 If\[f\left( x \right) = c\], they consist of all real numbers, there are no restrictions on the input. The only output value is the constant\[{\text{c}}\], so the range of the set \[\left\{ c \right\}\] that contains this single element

Range function: The range of a function is the complete set of all possible resulting values of the dependent variable of
For example:
Here: It is a set in the form of (\[{\text{x,y}}\]): $ \left\{ {( - 3,5),( - 2,5)( - 1,5)(2,5)(1,5)(2,5)} \right\} $
The values of\[\;{\text{y -}}\]values for the range.
Then range $ = \left\{ 5 \right\} $

Note: \[y\left( x \right) = {\text{3}}\] is the constant function where the range is $ 3 $ and the domain is $ x $.