Question

Define centripetal force. Also write the expression for it.

Answer 1

Hint:In this question,we are going to define centripetal force and then derive the expression of it by taking an instance.

Complete step by step answer:
Centripetal force is defined as: the force that is necessary to keep an object moving in a curved path and that is directed inward toward the center of rotation. Whilst centrifugal force is the force which is faced in an outward direction.
Now to understand it let us discuss some examples.
-The force of gravity acting on a satellite in the orbit.
-The friction of the tires of a car
Now let us derive the formula for centripetal force.

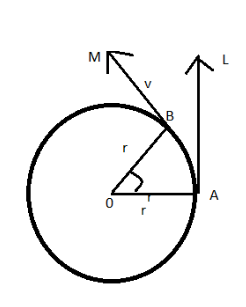
This is the diagram to derive the formula for centripetal force.
Let us consider a particle of mass m ‘m’ to be moving in a circle of radius ‘r’ with a constant speed ‘v’. Consider that the point is at A at any instant and then at B after a short time ‘t’.
Thus, AB=vt
When the time t is noticeably short, AB is almost a straight line and AOB is a triangle then triangles AOB and O’ab are similar.
Therefore,
\[\dfrac{{ab}}{{AB}} = \dfrac{{Oa'}}{{OA}}\]
Or, \[\dfrac{{ab}}{{vt}} = \dfrac{v}{r}\]
Since, \[(AB = vt\,and\,O'a = v\,,\,OA = r\])
Therefore,
\[\dfrac{{ab}}{t} = \dfrac{{{v^2}}}{r}\]
Or acceleration \[ = \dfrac{{{v^2}}}{r}\]…………(i)
We know that force is equal to mass multiplied by acceleration,
Therefore, Centripetal force \[ = \dfrac{{m{v^2}}}{r}\]……. (ii)
If \[\omega \] is the angular velocity, then \[v = r\omega \]
Therefore, centripetal force = \[mr{\omega ^2}\]……. (iii)
If the body takes n number of turns in one second, then \[\omega = 2\pi n\]

Therefore,the expression of centripetal force is \[4mr{\pi ^2}{n^2}\].


Note:Students often know the meaning of Centripetal force but do not know how to derive it. So students need to understand the meaning of centripetal force to be able to derive it.