Question

D and E are points on the sides AB and AC respectively such that BD = CE . If $\angle B = \angle C$ , show that $DE\parallel BC$ .

Answer 1

Hint: Use properties of triangles to find the equal sides and using the provided information break them to show that line BC is parallel to DE .

Complete step-by-step answer:

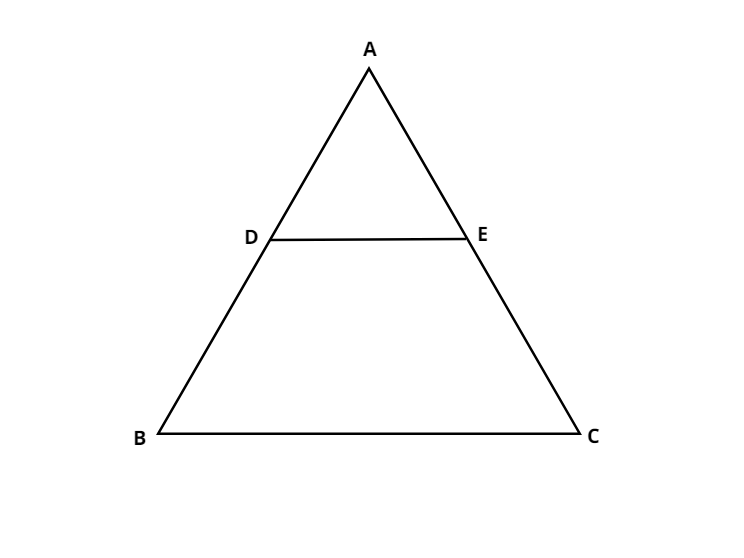
At first we draw a triangle ABC with point D and point E on sides AB and AC respectively .
 Since $\angle B = \angle C$
AB = AC ( sides opposite to equal angles of a triangle are equal )
Now we know that AB = AD + DB
and AC = AE + EC
AD + DB = AE + EC ( from above )
Cancelling out BD and EC as they are equal given in the question , we get
AD = AE
And BD = EC ( given )
Dividing both equations we get ,
$\dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{CE}}$
Now we know that If a line divides two sides of a triangle proportionally , then it is parallel to the third side ( Triangle Proportionality Theorem Converse )
Thus, we get $DE\parallel BC$.

Note: If you draw a parallel line to a side of a triangle that transects the other sides into two distinct points then the line divides those sides in proportion. This is called Basic Proportionality Theorem (BPT), the converse of which was used to prove sides DE and BC parallel. Basic properties of triangles should be used to solve such kinds of questions.