Question

Current time graph of different sources is given below, which one will have an RMS value ${{V}_{0}}$.

A)

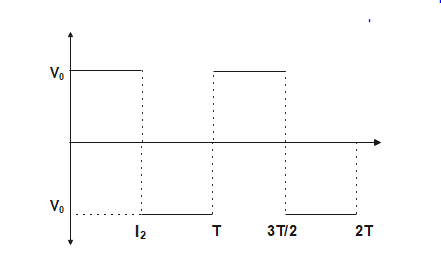
B)

C)

D)

Answer 1

Hint: The term “RMS” stands for Root mean squared (RMS).mostly define this because the amount of AC power that produces the same heating effect as an equivalent DC power , or something similar along these lines , but an RMS value is then just that. The RMS value is the root of the mean value of the squared function of the instantaneous values.

Complete step-by-step solution:
The RMS value is also called the effective value of a sinusoidal waveform that gives the same heating effect of an equivalent DC supply. So the RMS value of AC current is calculated by the maximum value of current divided by square root of 2.
The summation of the mean and RMS values of the DC and AC components, respectively, doesn’t describe the present signal.
The RMS value of a function is the root mean square value. It is the square root of the mean of the squares of the numbers. It is always positive and the RMS over all time of a periodic function is equal to the RMS of one period of the function.
RMS value for the figure in option A is:
${{V}_{RMS}}^{2}=\dfrac{1}{T}\int\limits_{0}^{T}{{{V}^{2}}dt}$
${{V}^{2}}_{RMS}=\dfrac{1}{T}[\int\limits_{0}^{\dfrac{T}{2}}{{{V}_{0}}^{2}dt+\int\limits_{0}^{\dfrac{T}{2}}{{{(-{{V}_{0}})}^{2}}dt}}$
${{V}_{RMS}}^{2}=\dfrac{1}{T}[2{{V}_{0}}^{2}\dfrac{T}{2}]$
${{V}^{2}}_{RMS}={{V}_{0}}^{2}$
So the correct option is A.

Note: Higher the mean values of current with the same RMS values, more will be the absorbed heat, the effect of the mean value of current depends on the RMS values. It is important to recall that by representing current either by mean value or by RMS value it does not mean that a similar Mean and RMS value would produce the same amount of heat.